
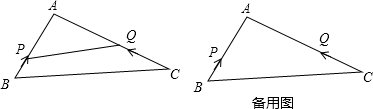
���� ��1������AB=6��AC=8��BC=12���жϳ���ABCΪֱ�������Σ����˶���ʾ��AP��AQ���ɣ�
��2����֪�н���ȣ�Ҫ�����������ƣ��߳ɱ�����������������㣻
��3���ɡ�A=90�㣬Ҫ��ƽ���ı��Σ������APD=90�㣬ͬ����AQD=90�㣬���Ե�D��BC���е㣮
��� �⣺��1����AB=6��AC=8��BC=12��
���ABC����BCΪб�ߵ�ֱ�������Σ�
�ߡ�APQΪ���������Σ�
��AP=AQ��
��BP=t��CQ=2t��
��AP=6-t��AQ=8-2t��
��6-t=8-2t��
��t=2��
��t=2ʱ����APQΪ���������Σ�
��2������A��P��QΪ��������������ABC���ƣ�
��$\frac{AP}{AB}=\frac{AQ}{AC}$��$\frac{AP}{AC}=\frac{AQ}{AB}$��
��$\frac{AP}{AB}=\frac{AQ}{AC}$ʱ��
��$\frac{6-t}{6}=\frac{8-2t}{8}$��
��t=0���ᣩ
��$\frac{AP}{AC}=\frac{AQ}{AB}$ʱ��
��$\frac{6-t}{8}=\frac{8-2t}{6}$��
��t=$\frac{14}{5}$��
����t=$\frac{14}{5}$ʱ��APQ�ס�ACB��
��3����ͼ��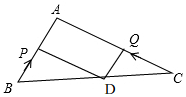
�����߶�BC���Ǵ���һ�㣬ʹ�ı���APDQ��ƽ���ı��Σ�
��PD��AQ��PD=AQ��
$\frac{PD}{AC}=\frac{PB}{AB}$=$\frac{CD}{BC}$
��$\frac{AQ}{AC}=\frac{BP}{AB}$��
��$\frac{8-2t}{8}=\frac{t}{6}$
��t=2.4
��PB=2.4��
��$\frac{2.4}{6}=\frac{CD}{12}$
��CD=4.8��
�������ڵ�D��CD=4.8ʱ���ı���APDQ��ƽ���ı��Σ�
���� �����������������ۺ��⣬��Ҫ�������������ε����ʺ��ж����Ȿ��Ĺؼ����ҵ����ƣ�������ѵ��Ƿ�������㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
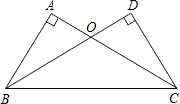 ��ͼ���ڡ�ABC�͡�DCB�У���A=��D=90�㣬AC=BD��AC��BD�ཻ�ڵ�O��
��ͼ���ڡ�ABC�͡�DCB�У���A=��D=90�㣬AC=BD��AC��BD�ཻ�ڵ�O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=2016x+m | B�� | y=$\frac{x}{2{x}^{2}+1}$+$\frac{m}{x}$ | C�� | y=x2-2016 | D�� | y=$\frac{{x}^{2}}{|x|}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
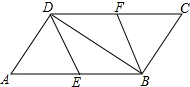 ��ͼ����?ABCD�У���E��F�ֱ�Ϊ��AB��CD���е㣬����DE��BF��BD��
��ͼ����?ABCD�У���E��F�ֱ�Ϊ��AB��CD���е㣬����DE��BF��BD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com