
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}-{b}^{2}}{(a+b)^{2}}$ | B. | $\frac{{b}^{2}-{a}^{2}}{a+b}$ | C. | $\frac{a+b}{a-b}$ | D. | $\frac{20(a-b)}{15(a+b)}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
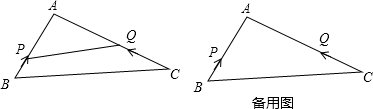
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
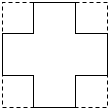 如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.
如图,将一块正方形铁片的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3.若设原铁片的边长为xcm,则根据题意可得关于x的方程(x-3×2)(x-3×2)×3=300.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
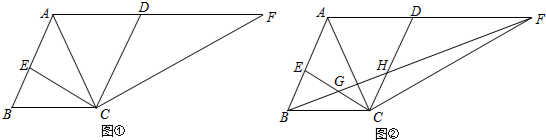
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
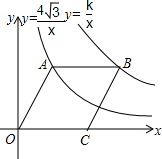 如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )
如图,点A在双曲线y=$\frac{4\sqrt{3}}{x}$(x>0)上,点B在双曲线y=$\frac{k}{x}$(x>0)上(点B在点A的右侧),且AB∥x轴,若四边形OABC是菱形,且∠AOC=60°,则k等于( )| A. | 6$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 9$\sqrt{3}$ | D. | 12$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com