
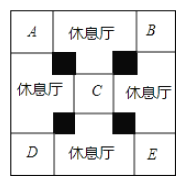
【题目】上海世博会中国国家馆模型的平面图如图所示,其外框是一个大正方形,中间四个大小相同的小正方形(阴影部分)是支撑展馆的核心筒,标记了字母的五个大小相同的正方形是展厅,剩余的四个大小相同的休息厅,已知核心筒的正方形边长比展厅的正方形边长的一半多1米.
(1)设展厅的正方形边长为![]() 米,用含
米,用含![]() 的代数式表示核心简的正方形边长为 米;
的代数式表示核心简的正方形边长为 米;
(2)设核心筒的正方形边长为![]() 米,求该模型的平面图外框大正方形的周长和每个休息厅的周长.(用含
米,求该模型的平面图外框大正方形的周长和每个休息厅的周长.(用含![]() 的代数式表示)
的代数式表示)
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
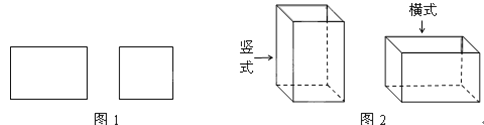
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图2所示的竖式与横式两种无盖的长方形纸箱(加工时接缝材料不计).
若该厂购进正方形纸板1000张,长方形纸板2000张,问竖式纸盒、横式纸盆各加工多少个,恰好能将购进的纸板全部用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
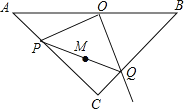
【题目】如图,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
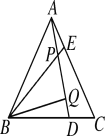
【题目】如图,△ABC为等边三角形,点D,E分别在BC,AC边上,且AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2) 求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
B.到点![]() 距离等于
距离等于![]() 的点的轨迹是以点
的点的轨迹是以点![]() 为圆心,半径长为
为圆心,半径长为![]() 的圆
的圆
C.到直线![]() 距离等于
距离等于![]() 的点的轨迹是两条平行于
的点的轨迹是两条平行于![]() 且与
且与![]() 的距离等于
的距离等于![]() 的直线
的直线
D.等腰三角形![]() 的底边
的底边![]() 固定,顶点
固定,顶点![]() 的轨迹是线段
的轨迹是线段![]() 的垂直平分线
的垂直平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学成绩好的同学,其计算的准确性一定还可以,七年级某班数学李老师很注重学生的计算过关检测,在学完《有理数》后,对全班同学进行检测过关.下表是这个班的童威同学一周内五天检测过关成绩(以85分为标准,高出部分用“+”表示,低于的部分用“-”表示)
星期 | 一 | 二 | 三 | 四 | 五 |
分数变化 |
|
|
|
|
|
(1)本周内童威同学哪天的检测成绩最高?是多少?哪天的检测成绩最低?是多少?
(2)请计算这5次检测成绩的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数![]() 的图象上,且x1<x2<x3,( )
的图象上,且x1<x2<x3,( )
A. 若![]() <
<![]() <
<![]() ,则
,则![]() +
+![]() +
+![]() >0B. 若
>0B. 若![]() <
<![]() <
<![]() ,则
,则![]()
![]()
![]() <0
<0
C. 若![]() <
<![]() <
<![]() ,则
,则![]() +
+![]() +
+![]() >0D. 若
>0D. 若![]() <
<![]() <
<![]() ,则
,则![]()
![]()
![]() <0
<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() 互为相反数,
互为相反数,![]() 互为倒数,且
互为倒数,且![]() 的立方等于它本身.
的立方等于它本身.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 试讨论:当
试讨论:当![]() 为有理数时,
为有理数时,![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由;
![]() 若
若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:折纸中的数学
问题情境:数学活动课上,老师让同学们折叠正方形纸片ABCD进行探究活动,兴趣小组的同学经过动手操作探究,提出了如下两个问题:
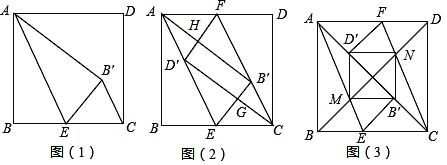
问题1:如图(1),若点E为BC的中点,设AE将正方形纸片ABCD折叠,点B的对应点为B′,连接B′C,求证:B′C∥AE.
问题2:如图(2),若点E,点F分别为边BC,边AD的中点,沿AE、CF将正方形纸片ABCD折叠,点B的对应点为B′,点D的对应点D′,D′F与AB′交于点H,B′E与CD′交于点G,求证:四边形D′GB′H为矩形.
(1)解决问题:请你对兴趣小组提出的两个问题进行证明.
(2)拓展探究:解决完兴趣小组提出的两个问题后,实践小组的同学们进行如下实践操作:如图(3),点E,点F分别为BC、AD上的点,将正方形纸片沿AE、CF折叠,使得点B落在对角线上的点B′处,点D落在对角线AC上的点D′处,AE与对角线BD的交点为M,CF与对角线BD的交点为N,分别连接MB′,B′N,D′N,D′M.他们认为四边形MB′ND′为正方形.
实践小组的同学们发现的结论是否正确?请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com