
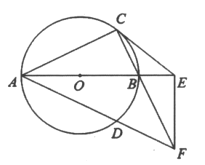
【题目】如图,AB为![]() 直径,C、D是
直径,C、D是![]() 上点,连结CB并延长与AD所在直线交于点F,
上点,连结CB并延长与AD所在直线交于点F,![]() ,垂足为点E,连结CE,且
,垂足为点E,连结CE,且![]() .
.
(1)证明:CE与![]() 相切;
相切;
(2)若![]() ,
,![]() ,求AD的长度.
,求AD的长度.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OC,根据等腰三角形的性质,对顶角的性质以及垂直的定义可得出∠BCE+∠ABC=90°,再根据∠OCB=∠OBC,得出∠OCB+∠BCE=90°,从而可得出结果;
(2)设![]() 的半径为r,则OA=OB=OC=r,则BE=8-2r,OE=8-r,根据
的半径为r,则OA=OB=OC=r,则BE=8-2r,OE=8-r,根据![]() =tan∠BFE,可得出EF=2BE=CE,在Rt△OCE中,利用勾股定理列方程可求出r的值.连接BD,又∠ACF=∠AEF=90°,则点A,C,E,F都在以AF为圆心的圆上,从而得出∠FAE=∠FCE,则tan∠BAD=
=tan∠BFE,可得出EF=2BE=CE,在Rt△OCE中,利用勾股定理列方程可求出r的值.连接BD,又∠ACF=∠AEF=90°,则点A,C,E,F都在以AF为圆心的圆上,从而得出∠FAE=∠FCE,则tan∠BAD=![]() ,结合勾股定理可求出AD的长.
,结合勾股定理可求出AD的长.
(1)证明:连接OC,
∵OB=OC,
∴∠OCB=∠OBC=∠EBF,
又EF⊥AB,
∴∠EFB+∠EBF=90°,
∴∠OCB+∠EFB=90°,
∵CE=EF,∴∠ECB=∠EFB,
∴∠OCB+∠ECB=90°,
∴∠OCE=90°,
∴CE与![]() 相切;
相切;
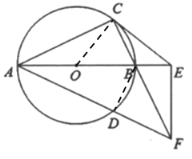
(2)解:连接BD,
设![]() 的半径为r,则OA=OB=OC=r,
的半径为r,则OA=OB=OC=r,
∴BE=AE-AB=8-2r,OE=AE-OA=8-r,
又![]() =tan∠BFE,
=tan∠BFE,
∴在Rt△BEF中,![]() ,
,
∴EF=2BE=16-4r=CE,
在Rt△OCE中,OC2+CE2=OE2,
∴r2+(16-4r)2=(8-r)2,
解得r=3或r=4,
当r=4时,16-4r=0,不符合题意,
∴r=3,
∴AB=6.
∵AB是![]() 的直径,
的直径,
∴∠ACF=∠AEF=90°,则点A,C,E,F都在以AF为直径的圆上,
∴∠FAE=∠FCE,
又![]() ,∴tan∠FAE=
,∴tan∠FAE=![]() ,即tan∠DAB=
,即tan∠DAB=![]() ,
,
∵AB是![]() 的直径,∴∠ADB=90°,
的直径,∴∠ADB=90°,
∴![]() ,
,
在Rt△ABD中,
AD2+BD2=AB2,
∴AD2+![]() =36,
=36,
∴AD=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
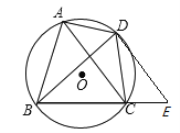
【题目】如图,四边形ABCD是⊙O的圆内接四边形,DE∥AC交BC的延长线于点E.
(1)求证:AB·DE=BD·DC;
(2)如果AD=CD,求证:DE为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“父母恩深重,恩怜无歇时”,每年5月的第二个星期日即为母亲节,节日前夕巴蜀中学学生会计划采购一批鲜花礼盒赠送给妈妈们.
(1)经过和花店卖家议价,可在原标价的基础上打八折购进,若在花店购买80个礼盒最多花费7680元,请求出每个礼盒在花店的最高标价;(用不等式解答)
(2)后来学生会了解到通过“大众点评”或“美团”同城配送会在(1)中花店最高售价的基础上降价25%,学生会计划在这两个网站上分别购买相同数量的礼盒,但实际购买过程中,“大众点评”网上的购买价格比原有价格上涨![]() m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了
m%,购买数量和原计划一样:“美团”网上的购买价格比原有价格下降了![]() m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了
m元,购买数量在原计划基础上增加15m%,最终,在两个网站的实际消费总额比原计划的预算总额增加了![]() m%,求出m的值.
m%,求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中仼意三个相邻格子中所填整数之和都相等.
|
|
|
| 5 | 4 | …… |
(1)可求得![]() _____;
_____;![]() _____;
_____;![]() _____.
_____.
(2)第2019个格子中的数为______;
(3)前2020个格子中所填整数之和为______.
(4)前![]() 个格子中所填整数之和是否可能为2020?若能,求出
个格子中所填整数之和是否可能为2020?若能,求出![]() 的值,若不能,请说明理由.
的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
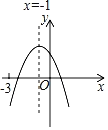
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2>4ac,②abc<0,③2a+b﹣c>0,④a+b+c<0.其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁5辆客车前往宁波东站接员工返岗.已知现有A、B两种客车,A型客车的载客量为45人/辆,每辆租金为400元;B型客车的载客量为30人/辆,每辆租金为280元.设租用A型客车为x辆,所需费用为y元.
(1)求y关于x的函数解析式;
(2)若该企业需要接的员工有205人,请求出租车费用最小值,并写出对应的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点坐标为(3,8),该二次函数图像的对称轴与
图象的顶点坐标为(3,8),该二次函数图像的对称轴与![]() 轴的交点为A,M是这个二次函数图像上的点,
轴的交点为A,M是这个二次函数图像上的点,![]() 是原点
是原点
(1)不等式![]() 是否成立?请说明理由;
是否成立?请说明理由;
(2)设![]() 是△AMO的面积,求满足
是△AMO的面积,求满足![]() 的所有点M的坐标.
的所有点M的坐标.
(3)将(2)中符号条件的点M联结起来构成怎样的特殊图形?写出两条这个特殊图形的性质.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com