
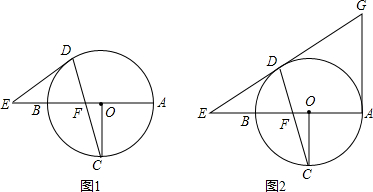
分析 (1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度
解答 (1)证明:连接OD,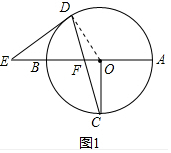
∵ED=EF,
∴∠EDF=∠EFD,
∵∠EFD=∠CFO,
∴∠EDF=∠CFO.
∵OD=OC,
∴∠ODF=∠OCF.
∵OC⊥AB,
∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,
∴ED为⊙O的切线;
(2)解:连接OD,过点D作DM⊥BA于点M,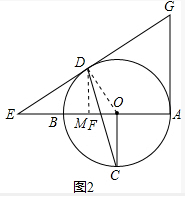
由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+2,
由勾股定理得,EO2=ED2+DO2,即(a+2)2=a2+62,
解得,a=8,即ED=8,EO=10.
∵sin∠EOD=$\frac{ED}{EO}$=$\frac{4}{5}$,cos∠EOD=$\frac{OD}{OE}$=$\frac{3}{5}$,
∴DM=OD•sin∠EOD=6×$\frac{4}{5}$=$\frac{24}{5}$,MO=OD•cos∠EOD=6×$\frac{3}{5}$=$\frac{18}{5}$,
∴EM=EO-MO=10-$\frac{18}{5}$=$\frac{32}{5}$,EA=EO+OA=10+6=16.
∵GA切⊙O于点A,
∴GA⊥EA,
∴DM∥GA,
∴△EDM∽△EGA,
∴$\frac{DM}{GA}$=$\frac{EM}{EA}$,即$\frac{\frac{24}{5}}{GA}$=$\frac{\frac{32}{5}}{16}$,
解得,GA=12.
点评 本题考查的是切线的判定、垂径定理和勾股定理的应用、等腰三角形的性质、角的三角函数值、相似三角形的判定及性质,解题的关键是:(1)通过等腰三角形的性质找出∠EDO=90°;(2)通过相似三角形的性质找出相似比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
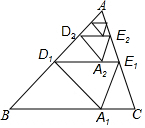 如图,对△ABC纸片进行如下操作:
如图,对△ABC纸片进行如下操作:| A. | $\frac{3}{2}$ | B. | $\frac{7}{4}$ | C. | $\frac{13}{8}$ | D. | $\frac{31}{16}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若$\sqrt{x-1}$+$\sqrt{1-x}$=y+4,则xy的平方根为1 | B. | 3-2$\sqrt{2}$的绝对值是2$\sqrt{2}$-3 | ||
| C. | 若$\sqrt{{a}^{2}b}$=-a$\sqrt{b}$成立,则a≤0且b≥0 | D. | 若$\sqrt{(1-a)^{2}}$+$\sqrt{(a-3)^{2}}$=2,则a≥3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
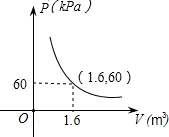 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )
某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数,其图象如图.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应( )| A. | 不小于$\frac{5}{4}$ m3 | B. | 小于$\frac{5}{4}$ m3 | C. | 不小于$\frac{4}{5}$ m3 | D. | 小于$\frac{4}{5}$ m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
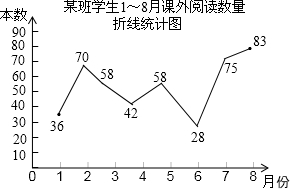 班长统计了今年1~8月“书香校园”活动中全班同学的课外阅读数量是(单位:本),绘制了如图折线统计图,下列说法正确的是( )
班长统计了今年1~8月“书香校园”活动中全班同学的课外阅读数量是(单位:本),绘制了如图折线统计图,下列说法正确的是( )| A. | 平均数是45 | B. | 众数是42 | C. | 中位数是58 | D. | 方差小于10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com