
 ȥ���������ҹ��ж�����������������������������ij����Ϊ���˽⡰������������Ҫ������������˲��������Ե��������������������������в�������ͳ�Ʊ���
ȥ���������ҹ��ж�����������������������������ij����Ϊ���˽⡰������������Ҫ������������˲��������Ե��������������������������в�������ͳ�Ʊ���| ��� | �۵� | Ƶ�� |
| A | ������ѹ�ͣ����������� | 120 |
| B | ����ҳ��࣬����ʪ�ȵ� | M |
| C | ����β���ŷ� | N |
| D | ������ɵ���Ⱦ | 180 |
| E | ���� | 90 |
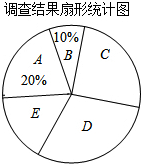
���� ��1������A����120�ˣ���ռ�İٷֱ���20%��������õ������������Ȼ����ݰٷֱȵ��������m��n��ֵ��
��2������75����Զ�Ӧ�İٷֱȼ�����ã�
��3�����C����ռ��Ƶ�ʼ�����ã�
��� �⣺��1��������������ǣ�120��20%=600���ˣ���
��m=600��10%=60��
n=600-120-60-180-90=150���ˣ���
����ͳ��ͼ��E����ռ�ٷֱ��ǣ�$\frac{90}{600}$=15%��
��2���������г�D�顰�۵㡱������������75��$\frac{90}{600}$-22.5����
��3��������һ�ˣ�����˳�C�顰�۵㡱�ĸ����ǣ�$\frac{150}{600}$=$\frac{1}{4}$��
���� ���⿼����Ƶ���ֲ���������ͳ��ͼ������ͳ��ͼ������ӳ����������ռ�İٷֱȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
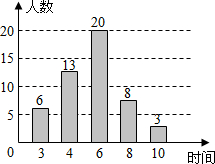 Ϊ�˽�ijС����ȫ��������Ŀ�չ�����ij־Ը�߶Ծ�ס�ڸ�С����50��������һ�ܵ���������ʱ�������ͳ�ƣ������Ƴ���ͼ��ʾ������ͳ��ͼ���������ݵ���������λ���ֱ��ǣ�������
Ϊ�˽�ijС����ȫ��������Ŀ�չ�����ij־Ը�߶Ծ�ס�ڸ�С����50��������һ�ܵ���������ʱ�������ͳ�ƣ������Ƴ���ͼ��ʾ������ͳ��ͼ���������ݵ���������λ���ֱ��ǣ�������| A�� | 6��4 | B�� | 6��6 | C�� | 4��4 | D�� | 4��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
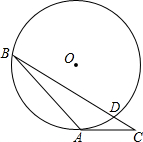 �ڡ�O�У�Բ�İ뾶Ϊ6����B=30�㣬AC�ǡ�O�����ߣ���CD����Сֵ�ǣ�������
�ڡ�O�У�Բ�İ뾶Ϊ6����B=30�㣬AC�ǡ�O�����ߣ���CD����Сֵ�ǣ�������| A�� | 1 | B�� | 3 | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
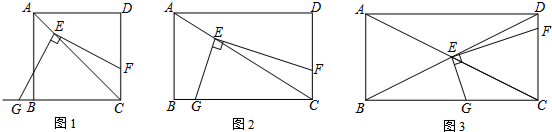
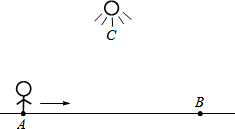 ���dz��á�y��x������������С��������ʾ��������֮��ı仯��ϵ��������һ���龳����ͼ��С���ӵ�A����·��C�����·���ֱ���ߵ���B������·��C�ľ���y�������A֮��ľ���x�ı仯���仯�����к�����y��x֮��ı仯��ϵ�����п����������龳���Ƶ��ǣ�������
���dz��á�y��x������������С��������ʾ��������֮��ı仯��ϵ��������һ���龳����ͼ��С���ӵ�A����·��C�����·���ֱ���ߵ���B������·��C�ľ���y�������A֮��ľ���x�ı仯���仯�����к�����y��x֮��ı仯��ϵ�����п����������龳���Ƶ��ǣ�������| A�� | y=x? | B�� | y=x+3 | C�� | y=$\frac{3}{x}$? | D�� | y=��x-3��2+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2a��2=2a2 | B�� | a6��a3=a3 | C�� | a3-a2=a6 | D�� | 3a2+2a3=5a3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com