
【题目】
(1)已知:如图,![]() 中,延长
中,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() 。
。
求证:![]() 。
。
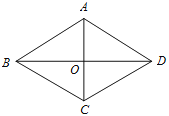
(2)如图,菱形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,已知
,已知![]() ,
,![]() 。求菱形
。求菱形![]() 的周长。
的周长。
【答案】(1)证明见解析;(2)菱形的周长为20.
【解析】试题分析:(1)根据平行四边形的对边平行且相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠C=∠FBE,∠C=∠CBE,然后利用“角角边”证明即可;(2)根据菱形对角线互相垂直平分的性质,可以求得BO=OD=4,AO=OC=3,在Rt△AOB中,根据勾股定理可以求得AB的长,即可求菱形ABCD的周长.
试题解析:
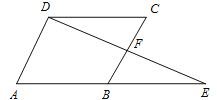
(1)证明:□ABCD中,
CD∥AB,CD=AB,
∴∠C=∠CBE, ∠CDF=∠E,
∵BE=AB, CD=AB
∴BE= CD
∴△BEF≌△CDF.
(2)解:菱形ABCD中,AC=6,BD=8
∴AC⊥BD,OA=OC=![]() =3,OB=OD=
=3,OB=OD=![]() =4
=4
Rt△AOB中,![]() ,
,
∴菱形的周长为20.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式,解答问题:
第1个等式:22﹣12=2×1+1=3;
第2个等式:32﹣22=2×2+1=5;
第3个等式:42﹣32=2×3+1=7;
第4个等式:;
…
第n个等式: . (n为整数,且n≥1)
(1)根据以上规律,在上边横线上写出第4个等式和第n个等式,并说明第n个等式成立;
(2)请从下面的A,B两题中任选一道题解答,我选择 A或B 题.
A.利用以上规律,计算20012﹣20002的值.
B.利用以上规律,求3+5+7+…+1999的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
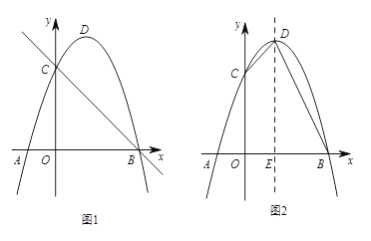
如图1,抛物线![]() 与x轴交于点
与x轴交于点![]() 、点
、点![]() (点
(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为顶点,已知点
为顶点,已知点![]() 、点
、点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 。
。
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上找一点
上方的抛物线上找一点![]() ,使
,使![]() 的面积最大,求
的面积最大,求![]() 点坐标;
点坐标;
(3)如图2,连结![]() 、
、![]() ,抛物线的对称轴与x轴交于点
,抛物线的对称轴与x轴交于点![]() 。过抛物线上一点
。过抛物线上一点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,求当
,求当![]() 时点
时点![]() 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( ) 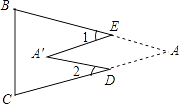
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的4×4方格中,每个小方格的边长都为1
(1)在图(1)中画出长度为 ![]() 的线段,要求线段的端点在格点上;
的线段,要求线段的端点在格点上;
(2)在图(2)中画出一个三条边长分别为3,2 ![]() ,
, ![]() 的三角形,使它的端点都在格点上.
的三角形,使它的端点都在格点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为解决大班额问题,对学校进行扩建,计划用三年时间对全县学校进行扩建和改造,2016年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2018年投资7.2亿元人民币,那么每年投资的增长率为( )
A. 20%、﹣220%B. 40%C. ﹣220%D. 20%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com