
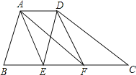
【题目】如图,在梯形![]() 中,
中,![]() 、
、![]() 两点分别在边
两点分别在边![]() 上.
上.![]() ,
,![]() ,且四边形
,且四边形![]() 是平行四边形.
是平行四边形.
![]() 请判断线段
请判断线段![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.
![]() 当
当![]() 时.请猜想四边形
时.请猜想四边形![]() 是什么特殊的平行四边形?并说明理由.
是什么特殊的平行四边形?并说明理由.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】等边△ABC的边BC在射线BD上,动点P在等边△ABC的BC边上(点P与BC不重合),连接AP.
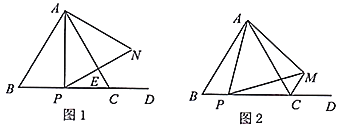
(1)如图1,当点P是BC的中点时,过点P作![]() 于E,并延长PE至N点,使得
于E,并延长PE至N点,使得![]() .①若
.①若![]() ,试求出AP的长度;
,试求出AP的长度;
②连接CN,求证![]() .
.
(2)如图2,若点M是△ABC的外角![]() 的角平分线上的一点,且
的角平分线上的一点,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( )个
①对角线互相平分的四边形是平行四边形;②等腰梯形在同一底上的两个内角相等;
③对角线互相垂直的四边形是菱形;④一组邻边相等的矩形是正方形.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
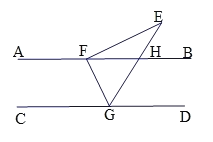
【题目】如图,AB// CD,Rt△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,∠EFG=90°,∠E=32°.
(1)∠FGE= °
(2)若GE平分∠FGD,求∠EFB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有3张边长为![]() 的正方形纸片(
的正方形纸片(![]() 类),5张边长为
类),5张边长为![]() 的矩形纸片(
的矩形纸片(![]() 类),5张边长为
类),5张边长为![]() 的正方形纸片(
的正方形纸片(![]() 类).
类).
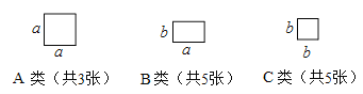
我们知道:多项式乘法的结果可以利用图形的面积表示.
例如:![]() 就能用图①或图②的面积表示.
就能用图①或图②的面积表示.
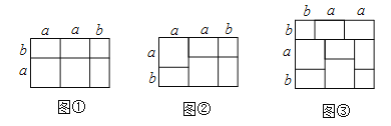
(1)请你写出图③所表示的一个等式:_______________;
(2)如果要拼一个长为![]() ,宽为
,宽为![]() 的长方形,则需要
的长方形,则需要![]() 类纸片_____张,需要
类纸片_____张,需要![]() 类纸片_____张,需要
类纸片_____张,需要![]() 类纸片_____张;
类纸片_____张;
(3)从这13张纸片中取出若干张,每类纸片至少取出一张,把取出的这些纸片拼成一个正方形(按原纸张进行无缝隙,无重叠拼接),则拼成的正方形的边长最长可以是_______(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
对这30个数据按组距3进行分组,并整理、描述和分析如下.
频数分布表
组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
销售额 |
|
|
|
|
|
|
|
频数 | 7 | 9 | 3 |
| 2 |
| 2 |
数据分析表
平均数 | 众数 | 中位数 |
20.3 |
| 18 |
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)若将月销售额不低于25万元确定为销售目标,则有 位营业员获得奖励;
(3)若想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com