
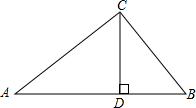
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )| A. | c•sin2α | B. | c•cos2α | C. | c•sinα•tanα | D. | c•sinα•cosα |
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).
如图,当小明沿坡度i=1:3的坡面由A到B行走了100米,那么小明行走的水平距离AC=30$\sqrt{10}$米.(结果可以用根号表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
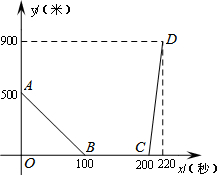 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x秒后两车间的距离为y千米,y关于x的函数关系如图所示,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com