
分析 (1)两个连续奇数的平方差等于8的倍数,由此得出第n个等式为(2n+1)2-(2n-1)2=8n,由此解决问题即可;
(2)理由(1)中的规律求得答案即可.
解答 解:(1)∵①32-12=8=8×1;
②52-32=16=8×2:
③72-52=24=8×3;
④92-72=32=8×4
…
∴第n个等式为(2n+1)2-(2n-1)2=8n;
(2)20132-20112=8048.
∵2×1006+1=2013,2×1006-1=2011,
∴n=1006.
故答案为:(2n+1)2-(2n-1)2=8n;8048,1006.
点评 此题主要考查了数字变化规律以及平方差公式,得出数字变化规律是解题关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
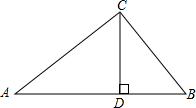 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )| A. | c•sin2α | B. | c•cos2α | C. | c•sinα•tanα | D. | c•sinα•cosα |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com