
分析 认真审题,利用作差法比较即可,作差时要注意观察题目特点,不要完全展开,运用整体思想可以简化运算.
解答 解:∵a1,a2,a3,…,a2015都是正整数,M=(a1+a2+a3+…+a2014)(a2+a3+…+a2015),N=(a1+a2+a3+…+a2015)(a2+a3+…+a2014),
∴M-N=(a1+a2+a3+…+a2014)(a2+a3+…+a2015)-(a1+a2+a3+…+a2015)(a2+a3+…+a2014)
=(a1+a2+a3+…+a2014)(a1+a2+a3+…+a2015)-a1(a1+a2+a3+…+a2014)-[(a1+a2+a3+…+a2015)(a1+a2+a3+…+a2014)-a1(a1+a2+a3+…+a2015)]
=(a1+a2+a3+…+a2014)(a1+a2+a3+…+a2015)-a1(a1+a2+a3+…+a2014)-(a1+a2+a3+…+a2015)(a1+a2+a3+…+a2014)+a1(a1+a2+a3+…+a2015)
=-a1(a1+a2+a3+…+a2014)+a1(a1+a2+a3+…+a2015)
=-a1(a1+a2+a3+…+a2014)+a1(a1+a2+a3+…+a2014)+a1•a2015
=a1•a2015>0,
∴M>N.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键,解答时要注意运用整体思想,简化运算过程,是很容易出错的题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
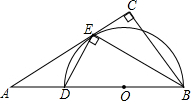 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
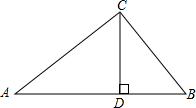 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AB=c,∠A=α,则CD长为( )| A. | c•sin2α | B. | c•cos2α | C. | c•sinα•tanα | D. | c•sinα•cosα |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com