
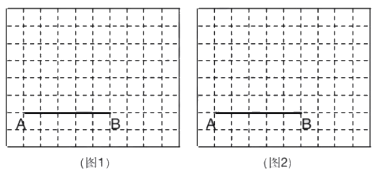
����Ŀ��ͼ1��ͼ2�ֱ���![]() ������������ÿ��С�����εı߳���Ϊ1��A��B������С�����εĶ����ϣ�����ͼ1��ͼ2�и�ȡ����C��D����C��D������С�����εĶ����ϣ���ʹ��A��B��C��DΪ������ı��ηֱ���������Ҫ��
������������ÿ��С�����εı߳���Ϊ1��A��B������С�����εĶ����ϣ�����ͼ1��ͼ2�и�ȡ����C��D����C��D������С�����εĶ����ϣ���ʹ��A��B��C��DΪ������ı��ηֱ���������Ҫ��
��1����ͼ1�л�һ������ABCD������AC����ʹ![]() ��
��
��2����ͼ2�л�һ����ABΪ�Խ��ߵ��ı���AEBF���Ҵ��ı���Ϊ��Գ�ͼ�Σ�![]() ����ֱ��д�������ı��ε������
����ֱ��д�������ı��ε������
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ����
����![]() ��
��![]() ���㣬������
���㣬������![]() ��һԪ���η���
��һԪ���η���![]() ��һ����Ϊ
��һ����Ϊ![]() ����
����![]() __________��
__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
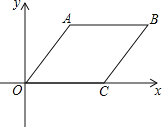
����Ŀ����ͼ��O������ԭ�㣬����OABC�Ķ���A������Ϊ![]() ������C��x����������ϣ���
������C��x����������ϣ���![]() �Ľ�ƽ��������ֱ�ߵĺ�����ϵʽΪ______��
�Ľ�ƽ��������ֱ�ߵĺ�����ϵʽΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ![]() �У��뾶Ϊ1��
�У��뾶Ϊ1��![]() ��
��![]() ���������
���������![]() ��������ֱ���
��������ֱ���![]() ���㣬ֱ��
���㣬ֱ��![]() ��
��![]() ��
��![]() ���
���![]() ��ֱ���
��ֱ���![]() ���㣮
���㣮

��l����ֱ��![]() ��
��![]() ����ʱ�������
����ʱ�������![]() ������͵�
������͵�![]() �����ꣻ
�����ꣻ
��2����ͼ2������![]() ���߶�
���߶�![]() ��ʱ��ֱ��
��ʱ��ֱ��![]() ��
��![]() ����
����![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ���Ϸ���������
���Ϸ���������![]() ��
��![]() �ᣬ��
�ᣬ��![]() ������һ��
������һ��![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
����ͼ3������![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() �ij���д�������̣�
�ij���д�������̣�
����ͼ2������![]() ���
���![]() ���غ�ʱ��
���غ�ʱ��![]() �ij��Ƿ����仯�����������仯�������
�ij��Ƿ����仯�����������仯�������![]() �ij���д�������̣��������仯����˵�����ɣ�
�ij���д�������̣��������仯����˵�����ɣ�
��3����ͼ4���ڣ�2���Ļ����ϣ�����![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ��
��![]() ������
������![]() ��
��![]() ���ӳ���ʱ�����õ�ʽֱ�ӱ�ʾ�߶�
���ӳ���ʱ�����õ�ʽֱ�ӱ�ʾ�߶�![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��������Դ�����ã����������ˮƽ��һ����Ҫ���֣�ij������˾�з��ļס������������豸���������¼���������������Ϊȼ�ϰ���ij�����������ӻ�����˾�����������������豸��������֪������������豸����360��Ԫ���������������豸����480��Ԫ������������豸������ͬ�������������豸�ĵ��ۺ�Ϊ140��Ԫ��
��1����������������豸���ۣ�
��2���������������������豸����ȼ�ϰ���������Ʒ���ۣ���֪ȼ�ϰ��ijɱ��������ɱ������ʳɱ���������ɣ��������ʳɱ�ռ�ܳɱ���40%��������ÿ��ȼ�ϰ����������ɱ������ʳɱ���![]() ������10Ԫ�����鷢�֣���ȼ�ϰ��ۼ�Ϊÿ��200Ԫ��ƽ��ÿ����۳�350�֣��������ۼ�ÿ����1Ԫ��ƽ��ÿ��ɶ��۳�5�֣����ۼ���ÿ��200Ԫ�����Ͻ��۷��Ȳ�����7%��
������10Ԫ�����鷢�֣���ȼ�ϰ��ۼ�Ϊÿ��200Ԫ��ƽ��ÿ����۳�350�֣��������ۼ�ÿ����1Ԫ��ƽ��ÿ��ɶ��۳�5�֣����ۼ���ÿ��200Ԫ�����Ͻ��۷��Ȳ�����7%��
��������������ʹ����ȼ�ϰ�����������ƽ��ÿ��ﵽ36080Ԫ����ÿ��ȼ�ϰ��ۼ�ӦΪ����Ԫ��
��ÿ��ȼ�ϰ��ۼ�ӦΪ����Ԫʱ������ȼ�ϰ�ƽ��ÿ����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
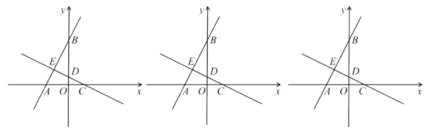
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���![]() Ϊ����ԭ�㣬
Ϊ����ԭ�㣬![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�A����
�ύ�ڵ�A����![]() ���ڵ�B����C����ֱ��AB�Ĵ��ߣ�����ΪE����
���ڵ�B����C����ֱ��AB�Ĵ��ߣ�����ΪE����![]() ���ڵ�D��
���ڵ�D��
��1����ֱ��CD�Ľ���ʽ��
��2����GΪ![]() �Ḻ������һ�㣬����EG������E��
�Ḻ������һ�㣬����EG������E��![]() ��
��![]() ���ڵ�H�����G������Ϊ
���ڵ�H�����G������Ϊ![]() ���߶�AH�ij�Ϊ
���߶�AH�ij�Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
֮��ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ��
��3������C��![]() ��Ĵ��ߣ�����G��
��Ĵ��ߣ�����G��![]() ��Ĵ��ߣ����߽��ڵ�M������H��
��Ĵ��ߣ����߽��ڵ�M������H��![]() �ڵ�N����ֱ��CD�ڵ�
�ڵ�N����ֱ��CD�ڵ�![]() ������MK����MKƽ��
������MK����MKƽ��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
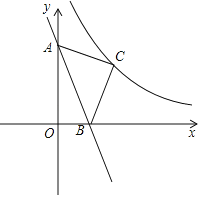
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ֱ��y����3x����ƽ��3����λ����y�ᡢx��ֱ��ڵ�A��B�����߶�ABΪб���ڵ�һ������������ֱ��������ABC��������������y��![]() ��x��0����ͼ����C����˷����������ı���ʽ��
��x��0����ͼ����C����˷����������ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�麬30��������CAB��30�����ǵ����ǰ��һ��������ƴ��һ�����ǰ�б��AB������������Բ��ֱ��MNǡ���غϣ�������������Ե�Ķ����Ǵ�N�㿪ʼ����N��Ķ���Ϊ0�㣩����������CP�Ƶ�C��CA��λ�ÿ�ʼ��˳ʱ�뷽����ÿ��2�ȵ��ٶ���ת��CBλ�ã�����ת�����У�����CP���������İ�Բ������E��
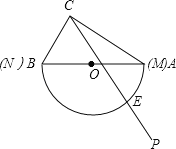
��1������ת7.5��ʱ������BE����˵����BE��CE��
��2����գ��ٵ�����CP������ABC������ʱ����E���Ķ������� ����
�ڵ�����CP������ABC������ʱ����E���Ķ������� ����
������תx���E����Ķ���Ϊy�ȣ���y��x�ĺ���ʽ��y���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������֣�
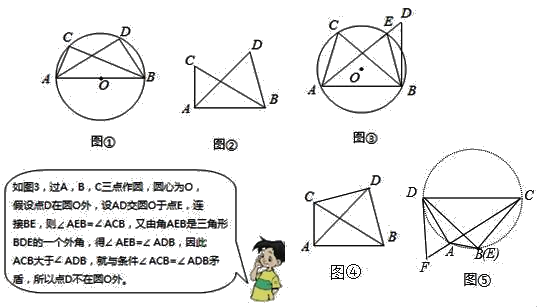
��ͼ��ACB=��ADB=90������ô��D�ھ���A��B��C�����Բ�ϣ���ͼ������
��ͼ�ڣ������ACB=��ADB=a��a��90��������C��D��AB��ͬ�ࣩ����ô��D���ھ���A��B��C�����Բ������֤����DҲ���ڡ�O�ڣ�
��Ӧ�ã�
���ã����֣��ͣ�˼�����еĽ��۽�����⣺
��1����ͼ�ܣ���֪��BCD=��BAD����CAD=40�������CBD�Ķ�����
��2����ͼ�ݣ����ı���ABCD�У���CAD=90��������CDF=90������CA�ӳ�����F����E��AB�ϣ���AED=��ADF��CD=3��EC=2����ED�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com