
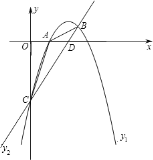
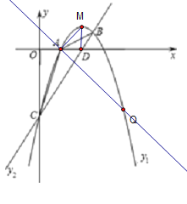
【题目】如图,已知抛物线y1=ax+bx+c的顶点坐标为M(2,1),且经过点B![]() ,抛物线对称轴左侧与
,抛物线对称轴左侧与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点C.
轴交于点C.

(1)求抛物线解析式y1和直线BC的解析式y2;
(2)连接AB、AC,求△ABC的面积.
(3)根据图象直接写出y1<y2时自变量![]() 的取值范围.
的取值范围.
(4)若点Q是抛物线上一点,且QA⊥MA,求点Q的坐标.
【答案】(1)y1=x2+4x3,![]() ;(2)
;(2)![]() ;(3)x<0或x>
;(3)x<0或x>![]() ;(4)Q(4,-3).
;(4)Q(4,-3).
【解析】
(1)设抛物线顶点式解析式y1=a(x-2)2+1,然后把点B的坐标代入求出a的值,即可求出抛物线解析式;令x=0求出点C的坐标,再设直线BC的解析式y2=kx+b(k≠0),利用待定系数法求一次函数解析式;
(2)令y=0,利用抛物线解析式求出点A的坐标,设直线BC与x轴的交点为D,利用直线BC的解析式求出点D的坐标,然后根据S△ABC=S△ABD+S△ACD,列式进行计算即可得解;
(3)根据图形,找出直线BC在抛物线上方部分的x的取值范围即可;
(4)连接MD,AM,过点A作AQ⊥AM,易得∠MAD=45°,即∠QAD=45°,从而得出Q点横纵坐标之间的关系,代入抛物线解析式求出Q点的坐标.
(1)∵抛物线的顶点坐标为(2,1),
∴y1=a(x2)2+1,
∵抛物线经过点![]() ,
,
∴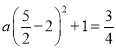 ,
,
解得a=1,
∴y1=(x2)2+1=x2+4x3,
当x=0,y=3,
∴C(0,3),
设直线BC解析式为y2=kx+b(k≠0),
则有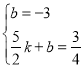 ,
,
解得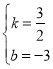
所以,直线BC的解析式为![]() ;
;
(2)对于y1=x2+4x3,当y=0时,x2+4x3=0,
即x24x+3=0,
解得x1=1,x2=3,
∴点A的坐标为(1,0),
设直线BC与x轴相交于D,
对于![]() ,当y=0时,
,当y=0时, ![]() ,
,
解得x=2,
∴点D的坐标为(2,0),
∴AD=21=1,
则S△ABC=S△ABD+S△ACD,
=![]()
=![]()
=![]() .
.
(3)由图得,当x<0或x>![]() 时,y1<y2.
时,y1<y2.
(4)连接MD,AM,过点A作AQ⊥AM.
∵M(2,1),D(2,0)
∴MD ⊥ x轴
∵A(1,0)
∴AD=MD,即△ADM为等腰直角三角形,
∴∠MAD=45°,即∠QAD=45°,
∴设Q(m,1-m)
则![]() ,解得m1=1(舍去),m2=4,
,解得m1=1(舍去),m2=4,
∴Q(4,-3).


 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD练习跑步,爸爸站在的某一个固定点处负责进行计时指导。假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图2所示,则爸爸所在的位置可能为图1的( )
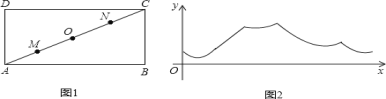
A. D点B. M点C. O点D. N点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有5张不透明的卡片,除正面上的图案不同外,其他均相同.将这5张卡片背面向上洗匀后放在桌面上.
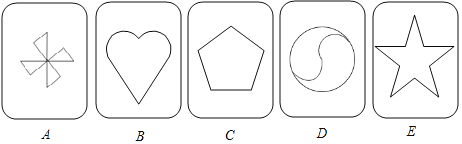
(1)从中随机抽取1张卡片,卡片上的图案是中心对称图形的概率为_____.
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用画树状图或列表的方法,求两次所抽取的卡片恰好都是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)抛物线与x轴的另一个交点坐标; ;
(2)方程ax2+bx+c=0的两个根是 ;
(3)不等式ax2+bx+c<0的解是 ;
(4)y随x的增大而减小的自变量x的取值范围是 ;
(5)求出抛物线的解析式及顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为x=1,给出下列结论:①abc>0;②b2=4ac;③4a+2b+c>0;④3a+c>0,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
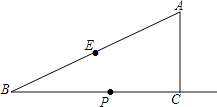
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的二元一次方程ax+b=y(a,b为常数且a≠0)
(1)该方程的解有 组;若a=﹣2,b=6,且x,y为非负整数,请直接写出该方程的解;
(2)若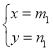 和
和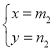 是该方程的两组解,且m1>m2
是该方程的两组解,且m1>m2
①若n1﹣n2=2(m2﹣m1),求a的值;
②若m1+m2=3b,n1+n2=ab+4,且b>2,请比较n1和n2大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com