
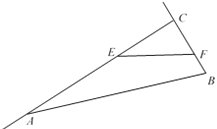
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=12 cm,BC=4 cm,点E从点C出发沿射线CA以每秒3cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
(1)若0<t <4,试问:t为何值时,以E、C、F为顶点的三角形与△ABC相似;
(2)若∠ACB的平分线CG交△ECF的外接圆于点G.
①试说明:当0<t <4时,CE、CF、CG在运动过程中,满足CE+CF=![]() CG.
CG.
②试探究:当t≥4时,CE、CF、CG的数量关系是否发生变化,并说明理由.
【答案】(1)t=2或0.4秒;(2)①证明见解析;②CE﹣CF=![]() CG.
CG.
【解析】
(1)0<t<4时,E和F分别在边AC和BC上,分成△EFC∽△ABC和△FEC∽△ABC两种情况,根据相似三角形的对应边的比相等即可求解;
(2)分成0<t<4和t≥4两种情况进行讨论,①当0<t<4时,证明△EGH≌△FGC,△CGH是等腰直角三角形,利用勾股定理即可求解,②当t≥4时,思路相同
解:(1)由题意,EC=3t,BF=t,FC=4﹣t
∵∠ECF=∠ACB,
∴以E、C、F为顶点的三角形与△ACB相似有两种情况:
当![]() 时,△EFC∽△ABC
时,△EFC∽△ABC
∴![]() ,解得t=2,
,解得t=2,
当![]() 时,△FEC∽△ABC
时,△FEC∽△ABC
∴![]() ,解得t=0.4.
,解得t=0.4.
∴当t=2或0.4秒时,以E、C、F为顶点的三角形与△ABC相似;
(2)①当0<t<4时,
过点G作GH⊥CG交AC于H,如图1:
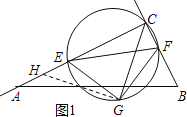
∵∠ACB=90°,
∴EF为△ECF的外接圆的直径,
∴∠EGF=90°,
∴∠EGH=∠FGC,
∵CG平分∠ACB,
∴∠ECG=∠FCG=45°
∴弧EG=弧FG
∴EG=FG
∵∠ECG=45°,
∴∠EHG=45°,
∴∠EHG=∠FCG,
在△EGH和△FGC中,
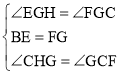 ,
,
∴△EGH≌△FGC.
∴EH=FC
∵∠EHG=∠ECG=45°,
∴CH=![]() CG
CG
∵CH=CE+EH,
∴CE+CF=![]() CG;
CG;
②当t≥4时,
过点G作GM⊥CG交AC于M,如图2:
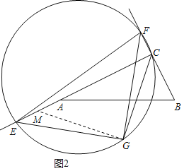
同理可得△EGM≌△FGC.
∴EM=FC
∵∠EMG=∠MCG=45°,
∴CM=![]() CG
CG
∵CM=CE﹣EM,
∴CE﹣CF=![]() CG.
CG.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:初中数学 来源: 题型:
【题目】随着生活水平的不断提高,越来越多的人选择到电影院观看电影,体验视觉盛宴,并且更多的人通过网上平台购票,既快捷又能享受更多优惠.某电影城2019年从网上购买![]() 张电影票的费用比现场购买
张电影票的费用比现场购买![]() 张电影票的费用少
张电影票的费用少![]() 元:从网上购买
元:从网上购买![]() 张电影票的费用和现场购买
张电影票的费用和现场购买![]() 张电影票的费用共
张电影票的费用共![]() 元.
元.
(1)求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?
(2)2019年五一当天,该电影城按照2019年网上购票和现场购票的价格销售电影票,当天售出的总票数为![]() 张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低
张.五一假期过后,观影人数出现下降,于是电影城决定从5月5日开始调整票价:现场购票价格下调,网上购票价格不变,结果发现,现场购票每张电影票的价格每降低![]() 元,售出总票数就比五一当天增加
元,售出总票数就比五一当天增加![]() 张.经统计,5月5日售出的总票数中有
张.经统计,5月5日售出的总票数中有![]() 的电影票通过网上售出,其余通过现场售出,且当天票房总收入为
的电影票通过网上售出,其余通过现场售出,且当天票房总收入为![]() 元,试求出5月5日当天现场购票每张电影票的价格为多少元?
元,试求出5月5日当天现场购票每张电影票的价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
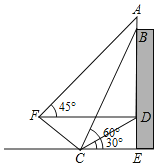
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于![]() ,超过
,超过![]() 时,所有这种水果的批发单价均为3元
时,所有这种水果的批发单价均为3元![]() .图中折线表示批发单价
.图中折线表示批发单价![]() (元
(元![]() )与质量
)与质量![]() 的函数关系.
的函数关系.
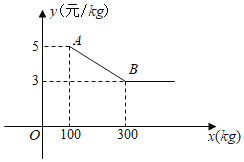
(1)求图中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)小李用800元一次可以批发这种水果的质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
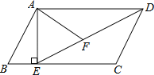
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=18,AD=![]() ,AF=
,AF=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商品销售某种商品,平均每天可售出20件,每件盈利50元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若每件商品降价2元,则平均每天可售出______件;
(2)当每件商品降价多少元时,该商品每天的销售利润为1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
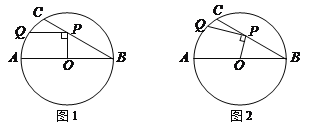
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.
(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;
(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于半径为
中,对于半径为![]() 的
的![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() ,则称
,则称![]() 为
为![]() 的“近外点”.
的“近外点”.
(1)当![]() 的半径为2时,点
的半径为2时,点![]() ,
,![]() ,
,![]() ,
,![]() 中,
中,![]() 的“近外点”是__________;
的“近外点”是__________;
(2)若点![]() 是
是![]() 的“近外点”,求
的“近外点”,求![]() 的半径
的半径![]() 的取值范围;
的取值范围;
(3)当![]() 的半径为2时,直线
的半径为2时,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若线段
,若线段![]() 上存在
上存在![]() 的“近外点”,直接写出
的“近外点”,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com