
【题目】“作差法”是常见的比较代数式大小的一种方法,即要比较代数式M、N的大小,只要作出它们的差M﹣N,若M﹣N>0,则M>N;若M﹣N=0,则M=N;若M﹣N<0,则M<N.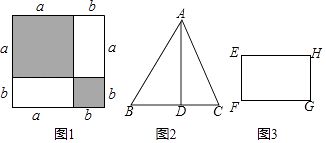
(1)如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个长方形,试比较来两个小正方形面积之和M与两个长方形面积之和N的大小.
(2)如图2,图3,△ABC中,AD⊥BC于D,AD=BC=2x﹣y,长方形EFGH中,长EH=2x﹣ ![]() y,宽EF=y,△ABC与长方形EFGH的面积分别为M、N,试比较M、N的大小,其中y>0,x>
y,宽EF=y,△ABC与长方形EFGH的面积分别为M、N,试比较M、N的大小,其中y>0,x> ![]() y且x≠y.
y且x≠y.
【答案】
(1)
解:根据题意得:M=a2+b2,N=ab+ab,
∴M﹣N=a2+b2﹣2ab=(a﹣b)2>0,
∴a≠b,
∴(a﹣b)2>0,
∴M﹣N>0,
∴M>N
(2)
解:在△ABC中,AD⊥BC于D,AD=BC=2x﹣y,
∴M= ![]() BCAD
BCAD
= ![]() (2x﹣y)2
(2x﹣y)2
=2x2﹣2xy+ ![]() y2,
y2,
在长方形EFGH中,长EH=2x﹣ ![]() y,宽EF=y,
y,宽EF=y,
∴N=EHEF
=(2x﹣ ![]() y)y
y)y
=2xy﹣ ![]() y2,
y2,
∴M﹣N=(2x2﹣2xy+ ![]() y2)﹣(2xy﹣
y2)﹣(2xy﹣ ![]() y2)
y2)
=2x2﹣2xy+ ![]() y2﹣2xy+
y2﹣2xy+ ![]() y2
y2
=2x2﹣4xy+2y2
=2(x2﹣2xy+y2)
=2(x﹣y)2,
∵x≠y,
∴(x﹣y)2>0,
∴2(x﹣y)2>0,
∴M﹣N>0,
即:M>N.
【解析】【解决问题】利用作差法比较M与N大小即可;【拓展延伸】利用作差法比较M与N大小即可;
【考点精析】本题主要考查了平行四边形的性质和平行四边形的判定的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
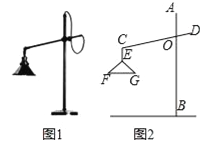
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)求这个二次函数的解析式;
(2)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
查看答案和解析>>
科目:初中数学 来源: 题型:
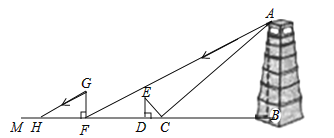
【题目】某市为了打造森林城市,树立城市新地标,实现绿色、共享发展理念,在城南建起了“望月阁”及环阁公园.小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度,来检验自己掌握知识和运用知识的能力.他们经过观察发现,观测点与“望月阁”底部间的距离不易测得,因此经过研究需要两次测量,于是他们首先用平面镜进行测量.方法如下:如图,小芳在小亮和“望月阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米,然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.
如图,已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
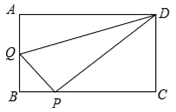
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6cm,BC=4cm,点P从点A出发(不含点A),沿A→B→C→D运动,同时,点Q从点B出发(不含点B),沿B→C→D运动,当点P到达点B时,点Q恰好到达点C,已知点P每秒比点Q每秒多运动1cm,当其中一点到达点D(不含点D)时,另一点停止运动.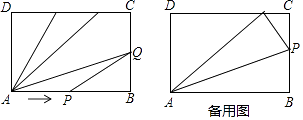
(1)求P、Q两点的速度;
(2)当其中一点到达点D时,另一点距离D点 cm(直接写答案);
(3)设点P、Q的运动时间为t(x),请用含t的代数式表示△APQ的面积为S(cm3),并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小彬一家人在2013年8月到北京旅游了4天,这4天的日期数(如8月1日的日期数为1)之和是38,则他们一家在北京旅游最后一天的日期数是( )
A.8号
B.9号
C.10号
D.11号
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com