
 反比例函数y=$\frac{1-m}{x}$的图象如图所示,以下结论正确的是( )
反比例函数y=$\frac{1-m}{x}$的图象如图所示,以下结论正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②③④ | D. | ①④ |
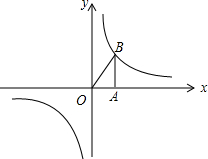
分析 根据函数的图象可知反比例函数y=$\frac{1-m}{x}$的图象在一、三象限,在每个象限内y随x的增大而减小,函数的图象关于原点对称,从而可以判断题目中的结论正确与否.
解答 解:由图象可知,反比例函数y=$\frac{1-m}{x}$在一、三象限,则1-m>0,得m<1,故①正确;
由图象可知,反比例函数y=$\frac{1-m}{x}$在每个象限内y随x的增大而减小,故②错误;
设点A的坐标为(a,0)点B的坐标为(b,$\frac{1-m}{b}$),则${S}_{△}=\frac{|a|×|\frac{1-m}{b}|}{2}$=$|\frac{a-am}{2b}|$,故③错误;
因为反比例函数的图象关于原点对称,故若P(x,y)在图象上,则P′(-x,-y)也在图象上,故④正确;
由上可得,结论正确的是①④,
故选D.
点评 本题考查反比例函数的性质,解题的关键是明确反比例函数的性质,利用反比例函数的性质可以解答具体的问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$x2 | B. | y=(x+0.5)2+2 | C. | y=(x-0.5)2+2 | D. | y=x2-2x-0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
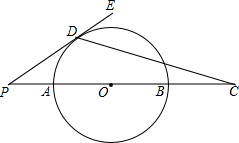 如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )
如图,AB是⊙O的半径,点P是BA延长线上一点,PE切⊙O于点D,延长PB至C,PA:AB:BC=1:3:1,则sin∠CDE的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{\sqrt{13}}{13}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{13}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com