
【题目】已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.
(1)求扇形OBC的面积(结果保留π);
(2)求证:CD是⊙O的切线.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB、下列确定P点的方法正确的是( )

A.P为∠A、∠B两角平分线的交点
B.P为AC、AB两边上的高的交点
C.P为∠A的角平分线与AB的垂直平分线的交点
D.P为AC、AB两边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:相似三角形对应边上的中线之比等于相似比.
要求:①根据给出的△ABC及线段A'B′,∠A′(∠A′=∠A),以线段A′B′为一边,在给出的图形上用尺规作出△A'B′C′,使得△A'B′C′∽△ABC,不写作法,保留作图痕迹;
②在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
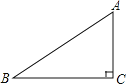
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.
(1)以直线BC为轴,把△ABC旋转一周,求所得圆锥的底面圆周长.
(2)以直线AC为轴,把△ABC旋转一周,求所得圆锥的侧面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 与反比例函数
与反比例函数![]() 的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且
的图像交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且![]() ⊥
⊥![]() .
.

(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)先在![]() 的内部求作点P,使点P到
的内部求作点P,使点P到![]() 的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
的两边OA、OB的距离相等,且PA=PB.(不写作法,保留作图痕迹,在图上标注清楚点P)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的爸爸和妈妈上山游玩,爸爸步行,妈妈乘坐缆车,相约在山顶缆车的终点会合.已知爸爸步行的路程是缆车所经线路长的2.5倍,妈妈在爸爸出发后50分钟才坐上缆车,缆车的平均速度为每分钟180米.图中的折现反映了爸爸行走的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系.
(分钟)之间的函数关系.

(1)爸爸行走的总路程是 米,他途中休息了 分钟;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是 ;
之间的函数关系式是 ;
(3)爸爸休息之后行走的速度是每分钟 米;
(4)当妈妈到达缆车终点是,爸爸离缆车终点的路程是 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践![]() 四边形旋转中的数学
四边形旋转中的数学
“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解答.
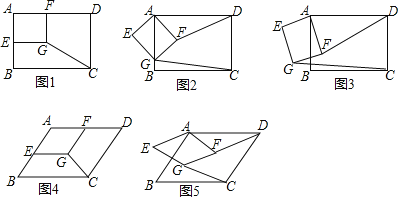
任务一:如图1,在矩形ABCD中,![]() ,
,![]() ,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
![]() 请直接写出CG的长是______.
请直接写出CG的长是______.
![]() 如图2,当矩形AEGF绕点A旋转
如图2,当矩形AEGF绕点A旋转![]() 比如顺时针旋转
比如顺时针旋转![]() 至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
![]() 当矩形AEGF绕点A旋转至如图3的位置时,
当矩形AEGF绕点A旋转至如图3的位置时,![]() 中DF与CG之间的数量关系是否还成立?请说明理由.
中DF与CG之间的数量关系是否还成立?请说明理由.
任务二:“智慧”数学小组对图形的旋转进行了拓展研究,如图4,在ABCD中,![]() ,
,![]() ,
,![]() ,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接
,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接![]() “智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
“智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
![]() 如图5,当AEGF绕点A旋转
如图5,当AEGF绕点A旋转![]() 比如顺时针旋转
比如顺时针旋转![]() ,其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系
,其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系![]() 请你直接写出这个特定的数量关系.
请你直接写出这个特定的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com