
【题目】如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面积.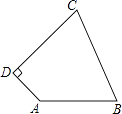
【答案】解:连接AC,过点C作CE⊥AB于点E. 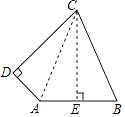
∵AD⊥CD,
∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,
AC= ![]() =
= ![]() =13.
=13.
∵BC=13,
∴AC=BC.
∵CE⊥AB,AB=10,
∴AE=BE= ![]() AB=
AB= ![]() ×10=5.
×10=5.
在Rt△CAE中,
CE= ![]() =
= ![]() =12.
=12.
∴S四边形ABCD=S△DAC+S△ABC= ![]() ×5×12+
×5×12+ ![]() ×10×12=30+60=90.
×10×12=30+60=90.
【解析】抓住题中关键的已知条件,AD⊥CD及CD=12,AD=5,因此连接AC,利用勾股定理求出AC的长,即可得出AC=BC,可知△CAB是等腰三角形,由此添加辅助线过点C作CE⊥AB于点E,利用勾股定理求出△CAB的高CE,要求四边形ABCD的面积,就转化为求△CAB和△ACD的面积,即可求解。
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对等腰三角形的判定的理解,了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+1与反比例函数y= ![]() 的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).
的图象交于A,B两点,已知点A的坐标为(1,a),点B的坐标为(b,﹣1).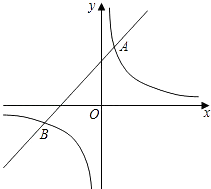
(1)求此反比例函数的解析式;
(2)当一次函数y=x+1的值大于反比例函数y= ![]() 的值时,求自变量x的取值范围.
的值时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且 ![]() =
= ![]() =
= ![]() ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2 ![]() ,则⊙O的半径为( )
,则⊙O的半径为( ) 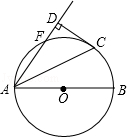
A.2 ![]()
B.4 ![]()
C.2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.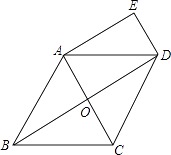
(1)求证:四边形AODE是矩形;
(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)一个学生有中国邮票和外国邮票共25张,中国邮票的张数比外国邮票的张数的2倍少2张,这个学生有中国邮票和外国邮票各多少张?
(2)甲乙二人相距18千米,二人同时出发相向而行,1小时相遇;同时出发同向而行,甲3小时可以追上乙。求二人的平均速度各是多少?
(3)国家为九年义务教育期间的学生实行“两免一补”政策,下表是某地区某中学国家免费提供教科书补助的部分情况。
| 七 | 八 | 九 | 合计 |
每人免费补助金额(元) | 110 | 90 | 50 | —— |
人数(人) | 80 | 300 | ||
免费补助金额(元) | 4000 | 26200 |
请问该校七、八年级各有学生多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发.设甲与A地相距![]() (km),乙与A地相距
(km),乙与A地相距![]() (km),甲离开A地的时间为x(h),
(km),甲离开A地的时间为x(h),![]() ,
,![]() 与x之间的函数图象如图所示.
与x之间的函数图象如图所示.

(1)甲的速度是 km/h;
(2)当1≤x≤5时,求![]() 关于x的函数解析式;
关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距 km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com