练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ﹣2的相反数是（　　）

    A． 2            B． ﹣2        C．             D．


    A．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


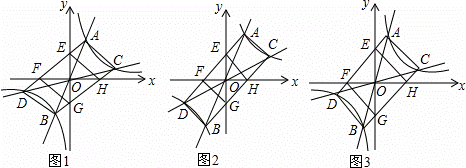
    如图1，直线y=k1x与反比例函数y=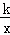（k≠0）的图象交于点A，B，直线y=k2x与反比例函数y=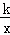的图象交于点C，D，且k1•k2≠0，k1≠k2，顺次连接A，D，B，C，AD，BC分别交x轴于点F，H，交y轴于点E，G，连接FG，EH．

    （1）四边形ADBC的形状是　 　；

    （2）如图2，若点A的坐标为（2，4），四边形AEHC是正方形，则k2=　 　；

    （3）如图3，若四边形EFGH为正方形，点A的坐标为（2，6），求点C的坐标；

    （4）判断：随着k1、k2取值的变化，四边形ADBC能否为正方形？若能，求点A的坐标；若不能，请简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知⊙O的割线PAB交⊙O于A，B两点，割线PCD经过圆心，若PA=3，AB=4，PO=5，则⊙O的半径为_____________.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    关于的二项式展开式中的常数项是       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     数列是递增的等比数列，且.

     (Ⅰ)若,求证：数列是等差数列;

    (Ⅱ)若……,求的最大值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点P在△ABC的边AC上，要判断△ABP∽△ACB，添加一个条件，不正确的是（　　）

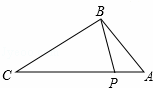
    A． ∠ABP=∠C  B． ∠APB=∠ABC     C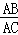． =   D． =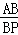

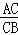
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC中，AB=AC，AB的垂直平分线交边AB于D点，交边AC于E点，若△ABC与△EBC的周长分别是40cm，24cm，则AB=　 　cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC沿着由点B到点E的方向，平移到△DEF，已知BC=5．EC=3，那么平移的距离为（　　）

    　

    A．

    2

    B．

    3

    C．

    5

    D．

    7

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


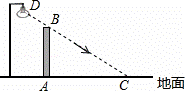
     如图，在水平地面上竖立着一面墙AB，墙外有一盏路灯D．光线DC恰好通过墙的最高点B，且与地面形成37°角．墙在灯光下的影子为线段AC，并测得AC=5.5米．

    （1）求墙AB的高度（结果精确到0.1米）；（参考数据：tan37°≈0.75，sin37°≈0.60，cos37°≈0.80）[来源:%&z~z^s@tep.com]

    （2）如果要缩短影子AC的长度，同时不能改变墙的高度和位置，请你写出两种不同的方法．

    查看答案和解析>>

    同步练习册答案