
如图1,直线y=k1x与反比例函数y=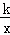 (k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=
(k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=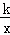 的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.
的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.
(1)四边形ADBC的形状是 ;
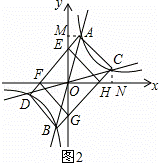
(2)如图2,若点A的坐标为(2,4),四边形AEHC是正方形,则k2= ;
(3)如图3,若四边形EFGH为正方形,点A的坐标为(2,6),求点C的坐标;
(4)判断:随着k1、k2取值的变化,四边形ADBC能否为正方形?若能,求点A的坐标;若不能,请简要说明理由.
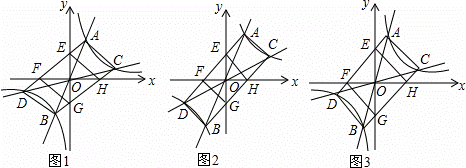
解:(1)∵正比例函数与反比例函数的图象均关于原点对称,
∴OA=OB,OC=OD,
∴四边形ADBC是平行四边形.
故答案为:平行四边形;
(2)如图1,过点A作AM⊥y轴,垂足为M,过点C作CN⊥x轴,垂足为N,
∵四边形AEHC是正方形,
∴DA⊥AC,
∴四边形ADBC是矩形,
∴OA=OC.
∴AM=CN,
∴C(4,2),
∴2=4k2,解得k2=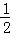 .
.
故答案为;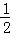 ;
;
(3)如图3所示,过点A作AM⊥y轴,垂足为M,过点C作CN⊥x轴,垂足为N,
∵四边形EFGH为正方形,
∴∠FEO=45°,EO=HO,
∴∠AEM=45°.
∵∠AME=90°,
∴∠EAM=∠AEM=45°.
∴AM=AE.
同理,CN=HN.
∵点A(2,6),
∴AM=ME=2,OM=6,
∴O E=OH=4.
E=OH=4.
设CN=HN=m,则点C的坐标为(4+m,m).
∵反比例函数y=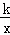 的图象过点C和点A(2,6),
的图象过点C和点A(2,6),
∴m•(4+m)=12,解得m1=2,m2=﹣6(舍去);
当m=2时,m+4=6,
∴点C的坐标为(6,2);
(4)不能.
∵反比例函数y=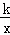 (k≠0)的图象不能与坐标轴相交,
(k≠0)的图象不能与坐标轴相交,
∴∠AOC<90°,
∴四边形ADBC的对角线不能互相垂直,
∴四边形ADBC不能是正方形.



 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
电视剧《铁血将军》在我市拍摄,该剧展示了抗日英雄范筑先的光辉形象.某校为了了解学生对“民族英雄范筑先”的知晓情况,从全校2400名学生中随机抽取了100名学生进行调查.在这次调查中,样本是( )
|
| A. | 2400名学生 |
|
| B. | 100名学生 |
|
| C. | 所抽取的100名学生对“民族英雄范筑先”的知晓情况 |
|
| D. | 每一名学生对“民族英雄范筑先”的知晓情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:
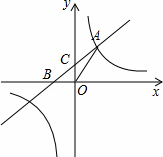
如图,直线y=x+b与双曲线y=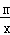 都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
都经过点A(2,3),直线y=x+b与x轴、y轴分别交于B、C两点.
(1)求直线和双曲线的函数关系式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
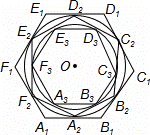
如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
|
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com