
 如图是由线段AB,CD,DF,BF,CA组成的平面图形,∠D=28°,则∠A+∠B+∠C+∠F的度数为( )
如图是由线段AB,CD,DF,BF,CA组成的平面图形,∠D=28°,则∠A+∠B+∠C+∠F的度数为( )| A. | 62° | B. | 152° | C. | 208° | D. | 236° |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 玩具型号 | A | B | C |
| 批发价(元/个) | 20 | 24 | 28 |
| 零售价(元/个) | 25 | 30 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
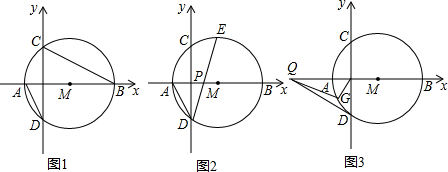
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴交于点O、M.对称轴为直线x=2,以OM为直径作圆A,以OM的长为边长作菱形ABCD,且点B、C在第四象限,点C在抛物线对称轴上,点D在y轴负半轴上;
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a>0)与x轴交于点O、M.对称轴为直线x=2,以OM为直径作圆A,以OM的长为边长作菱形ABCD,且点B、C在第四象限,点C在抛物线对称轴上,点D在y轴负半轴上;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 算术平方根等于自身的数只有1 | |
| B. | $\sqrt{\frac{1}{2}}$是最简二次根式 | |
| C. | 有一个角等于60°的三角形是等边三角形 | |
| D. | 两角及其夹边分别相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 角是轴对称图形,角平分线是它的对称轴 | |
| B. | 线段是轴对称图形,并且只有一条对称轴 | |
| C. | 三角形的一个外角等于它任意两个内角的和 | |
| D. | 在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com