Question

1．如图1，在平面直角坐标系中，点M的坐标为（3，0），以点M为圆心，5为半径的圆与坐标轴分别交于点A、B、C、D．
（1）△AOD与△COB相似吗？为什么？
（2）如图2，弦DE交x轴于点P，且BP：DP=3：2，求tan∠EDA；
（3）如图3，过点D作⊙M的切线，交x轴于点Q．点G是⊙M上的动点，问比值$\frac{GO}{GQ}$是否变化？若不变，请求出比值；若变化，请说明理由．

Answer 1

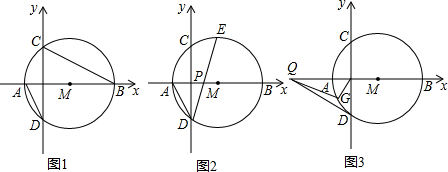
分析 （1）如图1，根据对顶角相等得到∠AOD=∠COB，根据圆周角定理得到∠ADO=∠OBC，则可判断△AOD∽△COB；
（2）连结AE、BE、MD，如图2，先计算出OD=2，再利用勾股定理计算出OD=4，AD=2$\sqrt{5}$，接着证明△PBE∽△PDA，利用相似比可计算出BE=3$\sqrt{5}$，然后根据勾股可计算出AE=$\sqrt{55}$，再利用正切的定义得到tan∠ABE=$\frac{\sqrt{11}}{3}$，于是得到tan∠EDA=$\frac{\sqrt{11}}{3}$；
（3）如图3，连结MD、MG，根据切线的性质得∠MDQ=90°，由∠ODM=∠OQD，则可判断Rt△ODM∽Rt△OQD，利用相似比可计算出OQ=$\frac{16}{3}$，讨论：当G点与A点重合时，易得$\frac{OG}{QG}$=$\frac{OA}{AQ}$=$\frac{3}{5}$；当G点与B点重合时，$\frac{OG}{QG}$=$\frac{3}{5}$；
当G点不与A、B重合时，先证明△MOD∽△MDQ得到即MD²=MO•MQ，由于MD=MG，则MG²=MO•MQ，加上∠OMG=∠GMQ，则可判断△MOG∽△MGQ，利用相似比可得$\frac{OG}{QG}$=$\frac{OM}{MG}$=$\frac{3}{5}$，于是得到$\frac{GO}{GQ}$的值不变，比值为$\frac{3}{5}$．

解答 解：（1）△AOD与△COB相似．理由如下：
如图1，
∵∠AOD=∠COB，∠ADO=∠OBC，
∴△AOD∽△COB；
（2）连结AE、BE、MD，如图2，
∵点M的坐标为（3，0），MA=MB=MD=5，
∴OD=2，
在Rt△ODM中，OD=$\sqrt{M{D}^{2}-O{M}^{2}}$=4，
在Rt△OAD中，AD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
∵∠PEB=∠PAD，∠PBE=∠PDA，
∴△PBE∽△PDA，
∴$\frac{BE}{AD}$=$\frac{PB}{PD}$=$\frac{3}{2}$，
∴BE=$\frac{3}{2}$×2$\sqrt{5}$=3$\sqrt{5}$，
在Rt△ABE中，
AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{1{0}^{2}-（3\sqrt{5}）^{2}}$=$\sqrt{55}$，
∴tan∠ABE=$\frac{AE}{BE}$=$\frac{\sqrt{55}}{3\sqrt{5}}$=$\frac{\sqrt{11}}{3}$，
∵∠EDA=∠ABE，
∴tan∠EDA=$\frac{\sqrt{11}}{3}$；
（3）如图3，连结MD、MG，
∵DQ为切线，
∴MD⊥QD，
∴∠MDQ=90°，
∵∠ODM=∠OQD，
∴Rt△ODM∽Rt△OQD，
∴OD：OQ=OM：OD，即4：OQ=3：4，
∴OQ=$\frac{16}{3}$，
当G点与A点重合时，$\frac{OG}{QG}$=$\frac{OA}{AQ}$=$\frac{2}{\frac{16}{3}-2}$=$\frac{3}{5}$；
当G点与B点重合时，$\frac{OG}{QG}$=$\frac{OB}{QB}$=$\frac{8}{\frac{16}{3}+8}$=$\frac{3}{5}$；
当G点不与A、B重合时，
∵∠OMD=∠DMQ，
∴△MOD∽△MDQ，
∴MO：MD=MD：MQ，即MD²=MO•MQ，
而MD=MG，
∴MG²=MO•MQ，
∵∠OMG=∠GMQ，
∴△MOG∽△MGQ，
∴$\frac{OG}{QG}$=$\frac{OM}{MG}$=$\frac{3}{5}$，
综上所述，$\frac{GO}{GQ}$的值不变，比值为$\frac{3}{5}$．

点评 本题考查了圆的综合题：熟练掌握圆周角定理和切线的性质；灵活应用相似三角形的判定与性质，会利用相似比和勾股定理计算线段的长．