
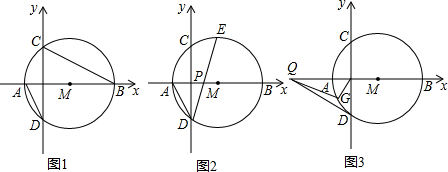
 如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C($\sqrt{3}$,1),点M是射线OC上一动点.
如图,矩形AOBC,点A、B分别在x、y轴上,对角线AB、OC交于点D,点C($\sqrt{3}$,1),点M是射线OC上一动点.分析 (1)利用点C坐标,即可求出相应角度,利用矩形性质,即可求出三角形CDA两个内角度数为60°,即可证明三角形是等边三角形.
(2)由等腰三角形性质,对三角形OAM三边关系进行讨论,分别求出三种情况下点M的坐标即可;
(3)做点A关于直线OC对称点,利用对称性可以求出最小值.
解答 解:(1)∵C($\sqrt{3}$,1),
∴AC=1,OA=$\sqrt{3}$,
∴OC=2,
∴∠COA=30°,∠OCA=60°,
∵矩形AOBC,
∴∠ABC=∠OCB=30°,
∴∠ADC=60°,
∴△ACD是等边三角形;
(2)△OAM是等腰三角形,
当OM=MA时,此时点M与点D重合,
∵C($\sqrt{3}$,1),点D为OC中点,
∴M($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
当OM1=OA时,做M1E⊥OA,垂足为E,如下图:
∴OM1=OA=$\sqrt{3}$,
由(1)知∠M1OA=30°,
∴M1E=$\frac{\sqrt{3}}{2}$,OE=$\frac{3}{2}$,
∴M1($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$).
当OA=AM2时,做M2F⊥OA,垂足为F,如上图:
AM2=$\sqrt{3}$,
由(1)知∠COA=∠AM2O=30°,
∴∠M2AF=60°,
∴AF=$\frac{\sqrt{3}}{2}$,M2F=$\frac{3}{2}$,
M2($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
综上所述:点M坐标为M($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)、($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)、($\frac{3\sqrt{3}}{2}$,$\frac{3}{2}$).
(3)存在,做点A关于直线OC对称点为G,如下图:
则AG⊥OC,且∠GOA=60°,OG=OA=$\sqrt{3}$,
∴ON=$\frac{\sqrt{3}}{2}$,GN=$\frac{3}{2}$,
∵点A、G关于直线OC对称,
∴MG=MA,
∴MA+MN=MG+MN,
∵N是OA上的动点,
∴当GN⊥x轴时,MA+MN最小,
∴存在MA+MN存在最小值,最小值为$\frac{3}{2}$.
点评 题目考查了一次函数综合应用,考查知识点包括:等腰三角形、线段最值、动点问题,解决此类题目关键是找到图形变换的规律,题目整体较难.适合学生压轴训练.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 玩具型号 | A | B | C |
| 批发价(元/个) | 20 | 24 | 28 |
| 零售价(元/个) | 25 | 30 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 算术平方根等于自身的数只有1 | |
| B. | $\sqrt{\frac{1}{2}}$是最简二次根式 | |
| C. | 有一个角等于60°的三角形是等边三角形 | |
| D. | 两角及其夹边分别相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一次函数y=kx+b的图象与两坐标轴的正半轴相交,则k,b的取值范围是( )
如图,一次函数y=kx+b的图象与两坐标轴的正半轴相交,则k,b的取值范围是( )| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com