Question

11．阅读下面材料：
小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB的度数；
小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．

（1）请你回答：图1中∠APB的度数等于150°．（直接写答案）
参考小伟同学思考问题的方法，解决下列问题：
如图3，在正方形ABCD内有一点P，且PA=2$\sqrt{2}$，PB=1，PD=$\sqrt{17}$．
（2）求∠APB的度数；
（3）求正方形的边长．

Answer 1

分析 （1）把△APB绕点A逆时针旋转60°得到△ACP′，由旋转的性质可得P′A=PA，P′C=PB，∠PAP′=60°，证出△APP′是等边三角形，由等边三角形的性质求出PP′=PA=3，∠AP′P=60°，再由勾股定理逆定理求出∠PP′C=90°，求出∠AP′C，即为∠APB的度数；
（2）把△APB绕点A逆时针旋转90°得到△ADP′，由旋转的性质可得P′A=PA，P′D=PB，∠PAP′=90°，证出△APP′是等腰直角三角形，由等腰直角三角形的性质求出PP′，∠AP′P=45°，再利用勾股定理逆定理求出∠PP′D=90°，然后求出∠AP′D，即为∠APB的度数；
（3）求出点P′、P、B三点共线，过点A作AE⊥PP′于E，根据等腰直角三角形的性质求出AE=PE=$\frac{1}{2}$PP′，然后求出BE，在Rt△ABE中，利用勾股定理求出AB即可．

解答 解：（1）如图2，把△APB绕点A逆时针旋转60°得到△ACP′，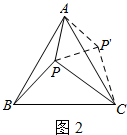
由旋转的性质，P′A=PA=3，P′D=PB=4，∠PAP′=60°，∠APB=∠AP′C，
∴△APP′是等边三角形，
∴PP′=PA=3，∠AP′P=60°，
∵PP′²+P′C²=3²+4²=25，PC²=5²=25，
∴PP′²+P′C²=PC²，
∴∠PP′C=90°，
∴∠AP′C=∠AP′P+∠PP′C=60°+90°=150°；
故∠APB=∠AP′C=150°；
故答案为：150°．
（2）如图3，把△APB绕点A逆时针旋转90°得到△ADP′，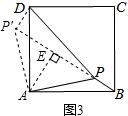
由旋转的性质，P′A=PA=2$\sqrt{2}$，P′D=PB=1，∠PAP′=90°，
∴△APP′是等腰直角三角形，
∴PP′=$\sqrt{2}$PA=4，∠AP′P=45°，
∵PP′²+P′D²=4²+1²=17，PD²=（$\sqrt{17}$^）2=17，
∴PP′²+P′D²=PD²，
∴∠PP′D=90°，
∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°，
故∠APB=∠AP′D=135°，
（3）∵∠APB+∠APP′=135°+45°=180°，
∴点P′、P、B三点共线，
过点A作AE⊥PP′于E，
则AE=PE=$\frac{1}{2}$PP′=$\frac{1}{2}$×4=2，
∴BE=PE+PB=2+1=3，
在Rt△ABE中，AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$．

点评 本题考查了旋转的性质，等边三角形的性质，正方形的性质，勾股定理以及勾股定理逆定理的应用，全等三角形的判定与性质，求正方形的边长有一定的难度，作辅助线构造出直角三角形是解题的关键．