
分析 (1)首先把分子和分母分解因式,把除法转化为乘法,然后进行约分即可求解;
(2)首先把括号内的分式通分相加,把除法转化为乘法,然后进行乘法运算即可化简,再代入数值计算即可.
解答 解:(1)原式=$\frac{(a-3)^{2}}{(2+b)(2-b)}$•$\frac{2+b}{3-a}$•$\frac{{a}^{2}}{3(a-3)}$
=$\frac{{a}^{2}}{3(2-b)}$;
(2)原式=$\frac{(x-2)^{2}+4x}{{x}^{2}-4}$•(x2-4)
=(x-2)2+4x
=x2-4x+4+4x
=x2+4.
当x=-3时,原式=9+4=13.
点评 本题考查了分式的混合运算,分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量m(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是$\sqrt{5}$.
如图,在Rt△OAB中,OA=2,AB=1,OA在数轴上,点O与原点重合,以原点为圆心,线段OB长为半径画弧,交数轴正半轴于一点,则这个点表示的实数是$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
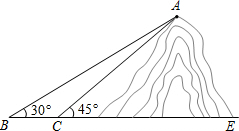 如图,小明想测山高和索道的长度,他在B处仰望山顶A,测得仰角∠B=30°.再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=45°.
如图,小明想测山高和索道的长度,他在B处仰望山顶A,测得仰角∠B=30°.再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com