
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
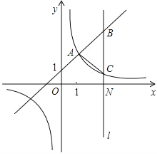
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
【答案】解:(1)将A(1,2)代入一次函数解析式得:k+1=2,即k=1,∴一次函数解析式为y=x+1。
将A(1,2)代入反比例解析式得:m=2,
∴反比例解析式为![]() 。
。
(2)设一次函数与x轴交于D点,过点A作AE垂直于x轴于点E,
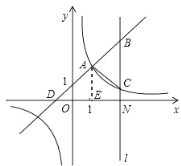
在y=x+1中,令y=0,求出x=﹣1,即OD=1。
∴A(1,2)。∴AE=2,OE=1。
∵N(3,0),∴到B横坐标为3。
将x=3代入一次函数得:y=4,
将x=3代入反比例解析式得:![]() ,
,
∴B(3,4),即ON=3,BN=4,C(3,![]() ),即CN=
),即CN=![]() ,
,
∴![]() 。
。
【解析】(1)将A坐标代入一次函数解析式中求出k的值,确定出一次函数解析式,将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例解析式;
(2)设一次函数与x轴交点为D点,过A作AE垂直于x轴,由△ABC面积=△BDN面积-△ADE面积-梯形AECN面积,求出即可。


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】以墙(长度不限)为一边,再用长为13m的铁丝为另外三边,围成面积为20![]() 的长方形.已知长大于宽,则长方形的长、宽分别是( )
的长方形.已知长大于宽,则长方形的长、宽分别是( )
A. 5m,4m或9m,2 m B. 9m,2m C. 10m,1.5m D. 8m,2.5m或5m,4m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和爸爸去登山,已知山脚到山顶的路程为300米,小明先走了一段路程,爸爸才开始出发,图中两条线段分别表示小明和爸爸离开山脚的路程![]() (米)与登山所用时间
(米)与登山所用时间![]() (分)的关系(从爸爸开始登山时计时),根据图象,下列说法错误的是( )
(分)的关系(从爸爸开始登山时计时),根据图象,下列说法错误的是( )
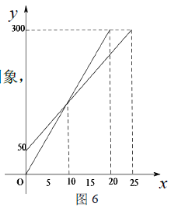
A.爸爸登山时,小明已经走了50米
B.爸爸走了5分钟,小明仍在爸爸的前面
C.小明比爸爸晚到5分钟
D.爸爸前10分钟登山的速度比小明慢,10分钟之后登山的速度比小明快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线M:y=ax2+bx+c(a≠0)经过A(﹣1,0),且顶点坐标为B(0,1).
(1)求抛物线M的函数表达式;
(2)设F(t,0)为x轴正半轴上一点,将抛物线M绕点F旋转180°得到抛物线M1.
①抛物线M1的顶点B1的坐标为 ;
②当抛物线M1与线段AB有公共点时,结合函数的图象,求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
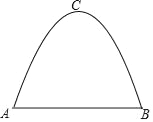
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com