
【题目】如图,在![]() 中,
中,![]() ,
,![]() .
.
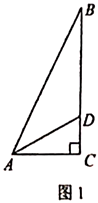
(1)如图1,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
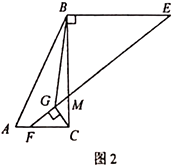
(2)如图2,点![]() 在边
在边![]() 上,过点
上,过点![]() 作
作![]() ,
,![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .求证:
.求证:![]() .
.
【答案】(1)3;(2)见解析.
【解析】
(1)根据勾股定理可得AC,进而可得BC与BD,然后根据三角形的面积公式计算即可;
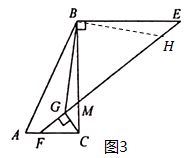
(2)过点B作BH⊥BG交EF于点H,如图3,则根据余角的性质可得∠CBG=∠EBH,由已知易得BE∥AC,于是∠E=∠EFC,由于![]() ,
,![]() ,则根据余角的性质得∠EFC=∠BCG,于是可得∠E=∠BCG,然后根据ASA可证△BCG≌△BEH,可得BG=BH,CG=EH,从而△BGH是等腰直角三角形,进一步即可证得结论.
,则根据余角的性质得∠EFC=∠BCG,于是可得∠E=∠BCG,然后根据ASA可证△BCG≌△BEH,可得BG=BH,CG=EH,从而△BGH是等腰直角三角形,进一步即可证得结论.
解:(1)在△ACD中,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴BC=4,BD=3,∴
,∴BC=4,BD=3,∴![]() ;
;
(2)过点B作BH⊥BG交EF于点H,如图3,则∠CBG+∠CBH=90°,
∵![]() ,∴∠EBH+∠CBH=90°,∴∠CBG=∠EBH,
,∴∠EBH+∠CBH=90°,∴∠CBG=∠EBH,
∵![]() ,
,![]() ,∴BE∥AC,∴∠E=∠EFC,
,∴BE∥AC,∴∠E=∠EFC,
∵![]() ,
,![]() ,∴∠EFC+∠FCG=90°,∠BCG+∠FCG=90°,
,∴∠EFC+∠FCG=90°,∠BCG+∠FCG=90°,
∴∠EFC=∠BCG,∴∠E=∠BCG,
在△BCG和△BEH中,∵∠CBG=∠EBH,BC=BE,∠BCG=∠E,∴△BCG≌△BEH(ASA),
∴BG=BH,CG=EH,
∴![]() ,
,
∴![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
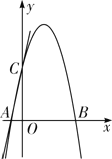
【题目】如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴,y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F、E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
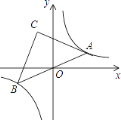
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
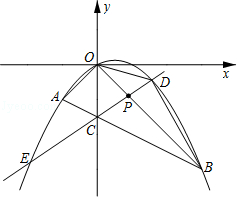
【题目】如图,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求抛物线的解析式;
(2)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.
①当△OPC为等腰三角形时,求点P的坐标;
②求△BOD 面积的最大值,并写出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC和等边△AEF都是半径为R的圆的内接三角形.
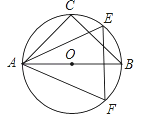
(1)求AF的长.
(2)通过对△ABC和△AEF的观察,请你先猜想谁的面积大,再证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好.
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2,并指出她与嘉嘉抽到勾股数的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+1(k≠0)与反比例函数![]() (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
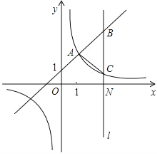
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线![]() .下列结论中,正确的是( )
.下列结论中,正确的是( )

A. abc>0 B. a+b=0 C. 2b+c>0 D. 4a+c<2b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com