
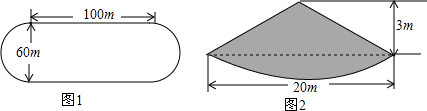
分析 (1)先求得如图1和图2所示场地中煤的体积,然后比较大小即可判断;
(2)先求得一辆B型车的载重体积,然后根据A型车的载重煤的体积+B型车的载重煤的体积=乙地煤的总体积列方程求解即可;
(3)A型车的速度为每分钟4xkm,B型车的速度为每分钟3xkm.根据A型车此时所行驶的路程比甲乙两地路程的一半多4km列方程求解即可.
解答 解:(1)甲场地的面积S=3.14×302+100×60=8826m2.
则甲场地需要煤的总体积=8826×0.04=353.04m3.
乙地有煤的体积=$\frac{1}{3}$×3.14×102×6=628m3.
∵353.04<628,
∴乙地的煤够用.
(2)一辆B型车的载重体积=15×$\frac{4}{3}$=20m3.
设需要B型车x辆,根据题意得;10×15+20x=628.
解得:x=23.9.
答:至少需要B型车24辆.
(3)设A型的速度为每分钟4y千米,B型的速度为每分钟3y千米.
根据题意得;4y×21=$\frac{1}{2}$×$\frac{1}{2}$×(68×3y+21×4y)+4.
解得;y=$\frac{1}{3}$.
甲乙两地的路程为(4×21×$\frac{1}{3}$-4)×2=48.
答:甲乙两地的路程为48千米.
点评 本题主要考查的是一元一次方程的应用,用含y的式子表示出甲乙两地之间的距离是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )
如图,身高1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为( )| A. | 4.8m | B. | 6.4m | C. | 8m | D. | 10m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$)-1=$\frac{3}{2}$ | B. | $\frac{1}{a}+\frac{1}{b}=\frac{2}{a+b}$ | C. | $\frac{{a}^{2}-{b}^{2}}{a-b}=a+b$ | D. | (-$\frac{1}{20}$)0=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 75m | B. | 50m | C. | 75$\sqrt{2}$m | D. | 50$\sqrt{2}$m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com