
 如图,该图是9×7的网格,网格中的每个小正方形的边长均为1,△ABC的顶点在小正方形的顶点上.
如图,该图是9×7的网格,网格中的每个小正方形的边长均为1,△ABC的顶点在小正方形的顶点上.分析 (1)利用网格特点和旋转的性质,作出点B,C的对应点B′、C′,即可得到△AB′C′;
(2)点B绕点A旋转至B′所经过的路线$\widehat{BB′}$是以点A为圆心,AB为半径,圆心角为90°的弧,然后根据弧长公式求解.
解答 解:(1)如图,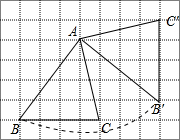 △AB′C′为所作;
△AB′C′为所作;
(2)∵△ABC绕点A逆时针旋转90°得到△AB′C′,
∴∠BAB′=90°,
∵AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴点B绕点A旋转至B′所经过的路线$\widehat{BB′}$的长=$\frac{90•π•5}{180}$=$\frac{5}{2}$π.
故答案为$\frac{5}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.
也考查了弧长公式.


科目:初中数学 来源: 题型:选择题
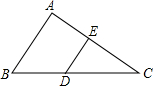 如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )
如图,△ABC,点D在BC上,DE∥AB交AC于点E,如果$\frac{AE}{EC}=\frac{2}{3}$,那么$\frac{DE}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
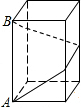 如图,长方体的底面是边长为1的正方形,长方体的高为3,如果用一根无弹力的细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短的是( )
如图,长方体的底面是边长为1的正方形,长方体的高为3,如果用一根无弹力的细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短的是( )| A. | 3 | B. | 4 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com