
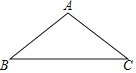
【题目】如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是_____.
【答案】![]() 或5或8.
或5或8.
【解析】
已知△ADE是等腰三角形,所以可以分3种情况讨论:①当AD=AE时,△ADE是等腰三角形.作AM⊥BC,垂足为M,利用勾股定理列方程可得结论;②当AD=DE时,四边形ABED是菱形,可得m=5;③当AE=DE时,此时C与E重合,m=8.
解:分3种情况讨论:
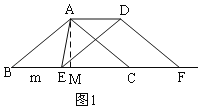
①当AD=AE时,如图1,过A作AM⊥BC于M,
∵AB=AC=5,BM=![]() BC=4,
BC=4,
∴AM=3,
由平移得:AB∥DE,AB=DE,
∴四边形ABED是平行四边形,
∴AD=BE=m,
∴AE=m,EM=4﹣m,
在Rt△AEM中,由勾股定理得:AE2=AM2+EM2,
∴m2=32+(4﹣m)2,
m=![]() ,
,
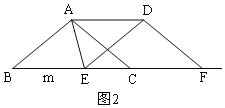
②当DE=AE时,如图2,
同理得:四边形ABED是平行四边形,
∴AD=BE=ED=AB=5,
即m=5;
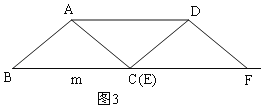
③当AC=DE时,如图3,此时C与E重合,
m=8;
综上所述:当m=![]() 或5或8时,△ADE是等腰三角形.
或5或8时,△ADE是等腰三角形.
故答案为:![]() 或5或8.
或5或8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
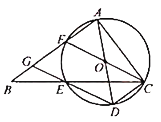
(1)求证:四边形DCFG是平行四边形;(2)当BE=4,CD=![]() AB时,求⊙O的直径长.
AB时,求⊙O的直径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,小张把容积为60升的油箱加满后自驾出行,行驶一段路程后进入服务区停车休息,休息后,小张离开服务区继续前行,为能顺利到达目的地,小张需在相距S千米的加油站加油.若小张从出发点到服务区休息点行驶的路程为200千米,且这期间平均油耗为每千米0.12升.
(1)求小张离开服务区休息点时,油箱内还有多少升汽油?
(2)记小张从离开服务区休息点到进入加油站加油期间的平均油耗为每千米a升,请写出S与a的函数关系式;若0.08≤a≤0.1,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=ax2+bx+c(a≠0)与x轴两个交点间的距离为6,称此抛物线为定弦抛物线.已知某定弦抛物线开口向上,对称轴为直线x=2,且通过(1,y1),(3,y2),(﹣1,y3),(﹣3,y4)四点,则y1,y2,y3,y4中为正数的是( )
A. y1B. y2C. y3D. y4
查看答案和解析>>
科目:初中数学 来源: 题型:
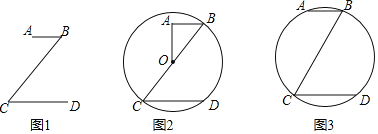
【题目】如图1,有一个“z”字图形,其中AB∥CD,AB:CD:BC=1:2:3.
(1)如图2,若以BC为直径的⊙O恰好经过点D,连结AO.
①求cosC.
②当AB=2时,求AO的长.
(2)如图3,当A,B,C,D四点恰好在同一个圆上时.求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
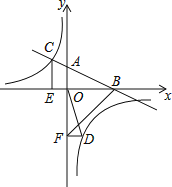
【题目】如图,在平面直角坐标系中,一次函数y=kx+b图象与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 在第二象限内的图象交于点C,CE⊥x轴,tan∠ABO=
在第二象限内的图象交于点C,CE⊥x轴,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函数与反比例函数的解析式;
(2)若点D是反比例函数在第四象限内图象上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,购进了甲、乙两种型号的新书柜来放置新买的图书,甲型号书柜共花了15000元,乙型号书柜共花了18000元,乙型号书柜比甲型号书柜单价便宜了300元,购买乙型号书柜的数量是甲型号书柜数量的2倍.求甲、乙型号书柜各购进多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦节前夕,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销量大,店主决定将玫瑰每枝降价2元促销,降价后80元可购买玫瑰的数量是原来可购买玫瑰数量的1.25倍.
(1)试问:降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于1000元的资金再次购进两种鲜花共180枝,康乃馨进价为6元/枝,玫瑰的进价是5元/枝。试问;至少需要购进多少枝玫瑰?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com