
【题目】若抛物线y=ax2+bx+c(a≠0)与x轴两个交点间的距离为6,称此抛物线为定弦抛物线.已知某定弦抛物线开口向上,对称轴为直线x=2,且通过(1,y1),(3,y2),(﹣1,y3),(﹣3,y4)四点,则y1,y2,y3,y4中为正数的是( )
A. y1B. y2C. y3D. y4
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
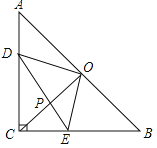
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为![]() ;④
;④![]() ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
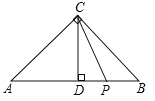
【题目】如图,在△ABC中,∠ACB=90°,∠A=45°,CD⊥AB于点D,点P在线段DB上,若AP2-PB2=48,则△PCD的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的网格中,有一格点△ABC(说明:顶点都在网格线交点处的三角形叫做格点三角形).
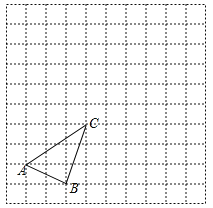
(1)将△ABC先向右平移5个单位,再向上平移2个单位,得到△A'B'C',请直接画出平移后的△A'B'C';
(2)将△A'B'C'绕点C'顺时针旋转90°,得到△A'B'C',请直接画出旋转后的△A'B'C';
(3)在(2)的旋转过程中,求点A'所经过的路线长(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

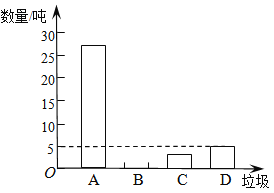
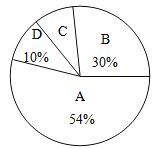
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=5,BC=8,若△ABC沿射线BC方向平移m个单位得到△DEF,顶点A,B,C分别与D,E,F对应,若以点A,D,E为顶点的三角形是等腰三角形,则m的值是_____.
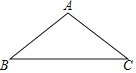
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某海监船以20km/h的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为_____km.
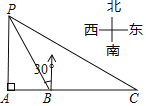
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;A4A0间的距离是_____;…按此规律运动到点A2019处,则点A2019与点A0间的距离是_____.
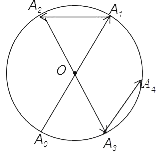
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com