
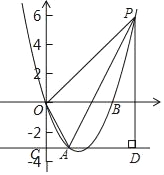
����Ŀ����ͼ����֪������y=ax2+bx��a��0������A��![]() ����3���͵�B��3
����3���͵�B��3![]() ��0��������A��ֱ��AC��x�ᣬ��y���ڵ�C��
��0��������A��ֱ��AC��x�ᣬ��y���ڵ�C��
��1���������ߵĽ���ʽ��
��2������������ȡһ��P������P��ֱ��AC�Ĵ��ߣ�����ΪD������OA��ʹ����A��D��PΪ���������������AOC���ƣ������Ӧ��P�����ꣻ
��3�����������Ƿ���ڵ�Q��ʹ��S��AOC=![]() S��AOQ�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
S��AOQ�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2��
x2��![]() x����2��P��������
x����2��P��������![]() ����
����![]() ����4
����4![]() ��6����
��6����![]() ����
����![]() ����0��0������3��Q��3
����0��0������3��Q��3![]() ��0����2
��0����2![]() ��15����
��15����
��������
��1����A��B������������߽���ʽ���a��b��ֵ������ȷ��������ʽ��
��2����P������x��![]() x2-
x2-![]() x������ʾ��AD��PD�������Ʒ���������ñ������x��ֵ������ȷ����P���ꣻ
x������ʾ��AD��PD�������Ʒ���������ñ������x��ֵ������ȷ����P���ꣻ
��3�����ڣ������֪������AOC��OA�ϵĸ�h����O��OM��OA����ȡOM=h����y�ύ�ڵ�N���ֱ�ȷ����M��N���꣬���ô���ϵ�������ֱ��MN����ʽ���������߽���ʽ�������Q���꼴�ɣ�
��1����A��![]() ����3���͵�B��3
����3���͵�B��3![]() ��0�����������ߵã�
��0�����������ߵã�![]() ��
��
��ã�a=![]() ��b=��
��b=��![]() ��
��
�������߽���ʽΪy=![]() x2��
x2��![]() x��
x��
��2����P��ֱ��AD�Ϸ�ʱ��
��P������x��![]() x2��
x2��![]() x��������AD=x��
x��������AD=x��![]() ��PD=
��PD=![]() x2��
x2��![]() x+3��
x+3��
����OCA�ס�ADPʱ��![]() ����
����![]() ��
��
�����ã�3x2��9![]() x+18=2
x+18=2![]() x��6����3x2��11
x��6����3x2��11![]() x+24=0��
x+24=0��
��ã�x=![]() ����x=
����x=![]() ��x=
��x=![]() ����ȥ����
����ȥ����
��ʱP��![]() ����
����![]() ����
����
����OCA�ס�PDAʱ��![]() ����
����![]() ��
��
�����ã�![]() x2��9x+6
x2��9x+6![]() =6x��6
=6x��6![]() ����x2��5
����x2��5![]() x+12=0��
x+12=0��
��ã�x=![]() ����x=4
����x=4![]() ��
��![]() ����ȥ����
����ȥ����
��ʱP��4![]() ��6����
��6����
����P��0��0��ʱ��Ҳ������OCA�ס�PDA��
��P��ֱ��AD�·�ʱ��ͬ���ɵã�P������Ϊ��![]() ����
����![]() ����
����
���ϣ�P������Ϊ��![]() ����
����![]() ����4
����4![]() ��6����
��6����![]() ����
����![]() ����0��0����
����0��0����
��3����Rt��AOC��OC=3��AC=![]() ��
��
���ݹ��ɶ����ã�OA=2![]() ��
��
��![]() OCAC=
OCAC=![]() OAh��
OAh��
��h=![]() ��
��
��S��AOC=![]() S��AOQ=
S��AOQ=![]() ��
��
���AOQ��OA�ϵĸ�Ϊ![]() ��
��
��O��OM��OA����ȡOM=![]() ����M��MN��OA����y���ڵ�N����ͼ��ʾ��
����M��MN��OA����y���ڵ�N����ͼ��ʾ��

��Rt��OMN��ON=2OM=9����N��0��9����
��M��MH��x�ᣬ
��Rt��OMH��MH=![]() OM=
OM=![]() ��OH=
��OH=![]() OM=
OM=![]() ����M��
����M��![]() ��
��![]() ����
����
��ֱ��MN����ʽΪy=kx+9��
��M�������ã�![]() =
=![]() k+9����k=��
k+9����k=��![]() ����y=��
����y=��![]() x+9��
x+9��
�����ã� ��
��
��ã�![]() ��
��![]() ����Q��3
����Q��3![]() ��0����2
��0����2![]() ��15����
��15����
���������ϴ��ڵ�Q��ʹ��S��AOC=![]() S��AOQ����ʱ��Q������Ϊ��3
S��AOQ����ʱ��Q������Ϊ��3![]() ��0����2
��0����2![]() ��15����
��15����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��ax![]() +bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x
+bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x![]() ��3x+5����a+b+c=__________��
��3x+5����a+b+c=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
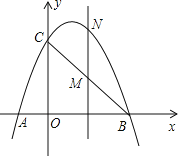
����Ŀ����ͼ����֪�����߾�����A(��1,0)��B(3,0)��C(0,3)���㡣
(1)�������ߵĽ���ʽ��
(2)��M���߶�BC�ϵĵ㣨����B��C�غϣ�����M��MN��y�ύ��������N����M�ĺ�����Ϊm������m�Ĵ���ʽ��ʾMN�ij���
(3)�ڣ�2���������£�����NB��NC���Ƿ����m��ʹ��BNC�������������ڣ���m��ֵ���������ڣ�˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+cͼ���һ���֣��ҹ���A��3��0�������κ���ͼ��ĶԳ�����x=1�����н��ۣ�
��b2��4ac����ac��0�� ����x��1ʱ��y��x���������С�� ��3a+c��0��������ʵ��m��a+b��am2+bm��
���н�����ȷ������ǣ�������
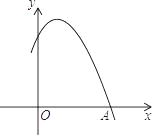
A. �٢ڢ� B. �٢ܢ� C. �ۢܢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
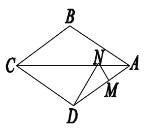
����Ŀ��������ABCD�У�M��AD���е㣬AB��4��N�ǶԽ���AC��һ���㣬��DMN ���ܳ���С��2+![]() ����BD�ij�Ϊ___________��
����BD�ij�Ϊ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
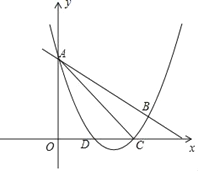
����Ŀ����ͼ��������y=![]() x2+mx+n��ֱ��y=��
x2+mx+n��ֱ��y=��![]() x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
x+3����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
��1���������ߵĹ�ϵʽ��tan��BAC��ֵ��
��2��PΪ��������һ���㣬����PA������P��PQ��OA��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ���������������ACB���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��3����AB����һ��M��ʹ��OM+DM��ֵ��С��ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
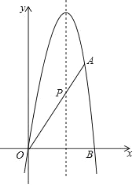
����Ŀ��������y=��![]() x2+bx+c��b��c���dz�����������O��0��0����A��4��4
x2+bx+c��b��c���dz�����������O��0��0����A��4��4![]() ������x�����һ����Ϊ��B���������߶Գ������߶�OA���ڵ�P��
������x�����һ����Ϊ��B���������߶Գ������߶�OA���ڵ�P��
��1����������ߵĽ���ʽ�Ͷ������ꣻ
��2������P��x���ƽ����l������Q��ֱ���ϵĶ��㣬����QB��
������O����ֱ��QB�ĶԳƵ�Ϊ��C������Cǡ����ֱ��l��ʱ�����Q�����ꣻ
������O����ֱ��QB�ĶԳƵ�Ϊ��D�����߶�AD�ij����ʱ�����Q�����ֱ꣨��д���𰸼��ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
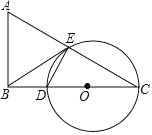
����Ŀ����ͼ������ABC �У���ABC��90�㣬��C��30�㣬AC �Ĵ�ֱƽ���߽� BC �ڵ� D����AC �ڵ� E��
(1)�ж� BE ����DCE �����Բ��O ��λ�ù�ϵ����˵�����ɣ�
(2)�� BE��![]() ��BD��1������DCE �����Բ��O ��ֱ����
��BD��1������DCE �����Բ��O ��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�ڽ�����O��BC����O��ֱ������D��BC�ӳ����ϵ�һ�㣬AD=AB������ACB=2��D��CD=2����ͼ1��

��1����֤��AD����O�����ߣ�
��2��AD= ��
��3������E����O�ϵ�һ�㣬AE��BC���ڵ�F���ҵ�E�ȷְ�ԲBCʱ����ͼ2������CF�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com