【题目】已知关于
的一元二次方程
（
）.
（1）求证：这个方程有两个不相等的实数根.
（2）如果这个方程的两个实数根分别为
，
，且
，求m的值.
【答案】(1)见解析；（2）m= 1．
【解析】
（1）只需证明根的判别式大于0即可．
（2）把等号左边整理（x1-3）（x2-3）=x1x2-3（x1+x2）+9，再把一元二次方程根与系数的关系代入列出方程解则可．
解：（1）△=（2m-1）2-4m（m-2）
=4m2-4m+1-4m2+8m
=4m+1
∵m＞0
∴4m+1＞0
所以方程有两个不相等的实数根．
（2）由根与系数的关系得
，
，
∵（x1-3）（x2-3）= x1x2-3（x1+x2）+9，
∴x1x2-3（x1+x2）+9=5m，
∴
两边同时乘以m并化简得，m-2-6m+3+9m=5m2
∴5m2-4m-1=0，
∴（5m+1）（m-1）=0，
解得m=1或
（舍去），
经检验m=1是方程的根．
所以m= 1．
开心练习课课练与单元检测系列答案科目：初中数学 来源： 题型：
【题目】如图，一次函数y=x+4的图象与反比例函数y=
（k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．
（1）求此反比例函数的表达式；
（2）若点P在x轴上，且S△ACP=
S△BOC，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，BC=9， CA=12，∠ABC的平分线BD交AC与点D， DE⊥DB交AB于点E．
（1）设⊙O是△BDE的外接圆，求证：AC是⊙O的切线；
（2）设⊙O交BC于点F，连结EF，求
的值．
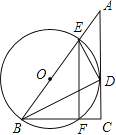
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形OABC的项点A、C分别在
、
轴的正半轴上，点B点反比例函数
（k≠0）的第一象限内的图象上，OA=3，OC=5，动点P在轴的上方，且满足
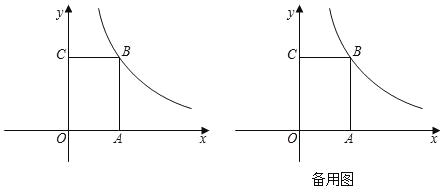
（1）若点P在这个反比例函数的图象上，求点P的坐标；
（2）连接PO、PA，求PO+PA的最小值；
（3）若点Q在平面内一点，使得以A、B、P、Q为顶点的四边形是菱形，则请你直接写出满足条件的所有点Q的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，他们分别以不同的速度匀速行驶.已知甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示，当乙到达终点A时，甲还需_________分钟到达终点B．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我市开展“美丽自宫，创卫同行”活动，某校倡议学生利用双休日在“花海”参加义务劳动，为了解同学们劳动情况，学校随机调查了部分同学的劳动时间，并用得到的数据绘制了不完整的统计图，根据图中信息回答下列问题：
（1）将条形统计图补充完整；
（2）扇形图中的“1.5小时”部分圆心角是多少度？
（3）求抽查的学生劳动时间的众数、中位数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，ABCD中，E、F分别是边AB、CD的中点．
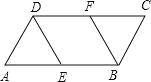
（1）求证：四边形EBFD是平行四边形；
（2）若AD=AE=2，∠A=60°，求四边形EBFD的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在等边
中，点D是边AC上一点，连接BD，将
绕着点B逆时针旋转
，得到
，连接ED，则下列结论中：① 
；② 
；③ 
；④ 
，其中正确结论的序号是
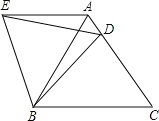
A. ①② B. ①③ C. ②③ D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=x2-ax-2a2（a为常数，且a≠0）．
（1）证明该二次函数的图象与x轴的正半轴、负半轴各有一个交点；
（2）若该二次函数的图象与y轴的交点坐标为（0，-2），试求该函数图象的顶点坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com