
 已知二次函数y1=x2+2x+m-5.
已知二次函数y1=x2+2x+m-5.分析 (1)由二次函数的图象与x轴有两个交点得出判别式△>0,得出不等式,解不等式即可;
(2)二次函数y1=x2+2x+m-5的图象经过把点B坐标代入二次函数解析式求出m的值,即可得出结果;点B(1,0);
(3)由图象可知:当y2<y1时,比较两个函数图象的位置,即可得出结果.
解答 解:(1)∵二次函数y1=x2+2x+m-5的图象与x轴有两个交点,
∴△>0,
∴22-4(m-5)>0,
解得:m<6;
(2)∵二次函数y1=x2+2x+m-5的图象经过点(1,0),
∴1+2+m-5=0,
解得:m=2,
∴它的表达式是y1=x2+2x-3,
∵当x=0时,y=-3,
∴C(0,-3);
(3)由图象可知:当y2<y1时,x的取值范围是x<-3或x>0.
点评 本题考查了二次函数图象上点的坐标特征、抛物线与x轴的交点;由题意求出二次函数的解析式是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 小聪用刻度尺画已知角的平分线,如图,在∠MAN两边上分别量取AB=AC,AE=AF,连接FC,EB交于点D,作射线AD,则图中全等的三角形共有4对.
小聪用刻度尺画已知角的平分线,如图,在∠MAN两边上分别量取AB=AC,AE=AF,连接FC,EB交于点D,作射线AD,则图中全等的三角形共有4对.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天一定会下雨 | |
| B. | 抛掷一枚均匀硬币,落地后正面朝上 | |
| C. | 任取两个正数,其和大于零 | |
| D. | 直角三角形的两锐角分别是20°和60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?($\sqrt{2}≈1.41,\sqrt{3}$≈1.73)
如图,某小区在规划改造期间,欲拆除小区广场边的一根电线杆AB,已知距电线杆AB水平距离14米处是观景台,即BD=14米,该观景台的坡面CD的坡角∠CDF的正切值为2,观景台的高CF为2米,在坡顶C处测得电线杆顶端A的仰角为30°,D、E之间是宽2米的人行道,如果以点B为圆心,以AB长为半径的圆形区域为危险区域.请你通过计算说明在拆除电线杆AB时,人行道是否在危险区域内?($\sqrt{2}≈1.41,\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
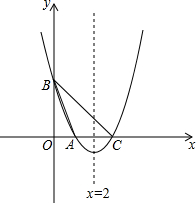 如图,抛物线y=x2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2.
如图,抛物线y=x2-bx+c与x轴交于A、C两点,与y轴交于B点,已知A点坐标为(1,0),抛物线的对称轴为直线x=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}(x+1)=3$ | B. | $\frac{1}{2}x+1=3$ | C. | 2x+1=3 | D. | 2(x+1)=3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com