
 如图,A、B两村和一条小河,要在河边L建一水厂Q向两村供水,若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述情况下的自来水厂厂址标出,并保留作图痕迹.
如图,A、B两村和一条小河,要在河边L建一水厂Q向两村供水,若要使自来水厂到两村的输水管用料最省,厂址Q应选在哪个位置?请将上述情况下的自来水厂厂址标出,并保留作图痕迹.  全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,点P的坐标是(3,4),直线l经过点P且平行于y轴,点Q从点A(3,10)出发,以每秒1个单位长的速度沿AP方向匀速运动.回答下列问题:
如图,平面直角坐标系中,点P的坐标是(3,4),直线l经过点P且平行于y轴,点Q从点A(3,10)出发,以每秒1个单位长的速度沿AP方向匀速运动.回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD的对角线AC和BD相交于点E,如果△CDE的面积为3,△BCE的面积为4,△AED的面积为6,那么△ABE的面积为8.
如图,四边形ABCD的对角线AC和BD相交于点E,如果△CDE的面积为3,△BCE的面积为4,△AED的面积为6,那么△ABE的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
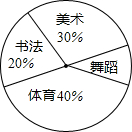 某校为了解学生的课余爱好,对全校1200名学生进行抽样调查,并把调查结果制成如图所示的统计图,由图可知,该校喜欢舞蹈的学生大约有120名.
某校为了解学生的课余爱好,对全校1200名学生进行抽样调查,并把调查结果制成如图所示的统计图,由图可知,该校喜欢舞蹈的学生大约有120名.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com