
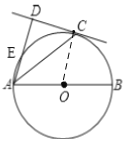
【题目】如图,点C在AB为直径的圆O上,AD与过点C的切线垂直,垂足为点D,AD交圆O于点E.
(1)求证:AC平分∠DAB;
(2)连接BE,若BE=6,sin∠CAD=![]() ,求圆O的半径.
,求圆O的半径.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)如图,连接OC,由切线性质及AD⊥CD可得AD//OC,得到∠DAC=∠ACO,根据等腰三角形的性质可得∠ACO=∠CAO,即可证明AC平分∠DAB;(2)如图,连接BE、BC,BE交OC于F,由∠D=∠DEB=∠DCF=90°,可得四边形DEFC是矩形,由垂径定理可知EF=![]() BE=3,进而可得CD=EF=3,根据∠CAD的正弦值可求出AC的长,由圆周角定理可得∠ACB=90°,利用∠BAC的三角函数值即可求出AB的长,即可得答案.
BE=3,进而可得CD=EF=3,根据∠CAD的正弦值可求出AC的长,由圆周角定理可得∠ACB=90°,利用∠BAC的三角函数值即可求出AB的长,即可得答案.
(1)如图,连接OC,
∵CD是⊙O的切线,OC为半径,
∴OC⊥CD,
∵AD⊥CD,
∴AD//OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠ACO=∠CAO
∴∠DAC=∠CAO,
∴AC平分∠DAB.
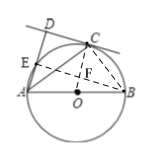
(2)如图,连接BE、BC,BE交OC于F,
∵AB是直径,∠AEB、∠ACB是AB所对圆周角,
∴∠AEB=90°,∠ACB=90°,
∵∠EDC=∠FCD=∠DEF=90°,
∴四边形DEFC是矩形,
∵OF⊥BE,OC是半径,BE是弦,
∴EF=![]() BE=3,
BE=3,
∴CD=EF=3,
∵sin∠CAD=![]() =
=![]() ,
,
∴AC=5,
∵sin∠CAD=![]() ,
,
∴cos∠CAD=![]() =
=![]() ,
,
∵∠CAD=∠CAB,
∴cos∠CAB=cos∠CAD=![]() =
=![]() ,
,
∴AB=![]() ,
,
∴OA=![]() AB=
AB=![]() .
.


科目:初中数学 来源: 题型:
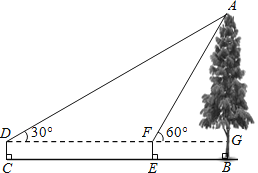
【题目】如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,![]() ≈1.732).
≈1.732).
查看答案和解析>>
科目:初中数学 来源: 题型:
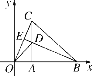
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
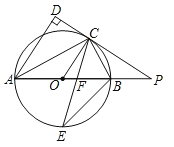
【题目】如图,已知![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上一点,
上一点,![]() 与过点
与过点![]() 的切线垂直,垂足为点
的切线垂直,垂足为点![]() ,直线
,直线![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,弦
,弦![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
(1)求证:![]() 平分
平分![]() ;
;
(2)求证:![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求圆
,求圆![]() 的半径长.
的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
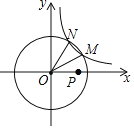
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是_____.
(k>0)的图象与半径为5的⊙O交于M、N两点,△MON的面积为3.5,若动点P在x轴上,则PM+PN的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程,①3x2+x=20,②2x2-3xy+4=0,③![]() ,④x2=0,⑤x2-3x-4=0.是一元二次方程的是( )
,④x2=0,⑤x2-3x-4=0.是一元二次方程的是( )
A. ①②B. ①②④⑤C. ①③④D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.

(l)若AB=1O,求FD的长;
(2)若AC=BC.求证:△CDE∽△DFE .
查看答案和解析>>
科目:初中数学 来源: 题型:
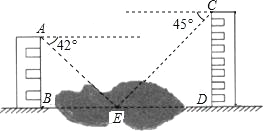
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com