练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列方程，①3x2+x=20，②2x2-3xy+4=0，③，④x2=0，⑤x2-3x-4=0．是一元二次方程的是（　　）

    A. ①②B. ①②④⑤C. ①③④D. ①④⑤

    【答案】D

    【解析】

    本题根据一元二次方程的定义解答．

    一元二次方程必须满足四个条件：

    （1）是整式方程；

    （2）只含有一个未知数．

    （3）未知数的最高次数是2；

    （4）化简后二次项系数不为0；

    由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．

    解：①由原方程得到：3x2+x-20=0，符合一元二次方程的定义．故①正确；

    ②2x2-3xy+4=0中含有两个未知数，属于二元二次方程．故②错误；

    ③属于分式方程．故③错误；

    ④x2=0，符合一元二次方程的定义．故④正确；

    ⑤x2-3x-4=0，符合一元二次方程的定义．故⑤正确；

    综上所述，正确的是①④⑤．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,在矩形ABCD中,AB：BC=3：5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.

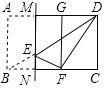
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O直径，P点为半径OA上异于O点和A点的一个点，过P点作与直径AB垂直的弦CD，连接AD，作BE⊥AB，OE∥AD交BE于E点，连接AE、DE、AE交CD于F点．

    （1）求证：DE为⊙O切线；

    （2）若⊙O的半径为3，sin∠ADP=，求AD；

    （3）请猜想PF与FD的数量关系，并加以证明．

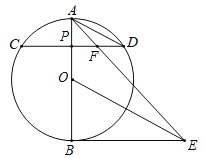
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C在AB为直径的圆O上，AD与过点C的切线垂直，垂足为点D，AD交圆O于点E.

    （1）求证：AC平分∠DAB；

    （2）连接BE，若BE=6，sin∠CAD=，求圆O的半径.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我省某地区为了了解2017年初中毕业生毕业去向，对部分九年级学生进行了抽样调查，就九年级学生毕业后的四种去向：A．读重点高中；B．读职业高中；C．直接进入社会就业；D．其他（如出国等）进行数据统计，并绘制了两幅不完整的统计图（如①图，如②图）

    （1）该地区共调查了_____名九年级学生；

    （2）将两幅统计图中不完整的部分补充完整；

    （3）若该地区2017年初中毕业生共有4000人，请估计该地区今年初中毕业生中读重点高中的学生人数．

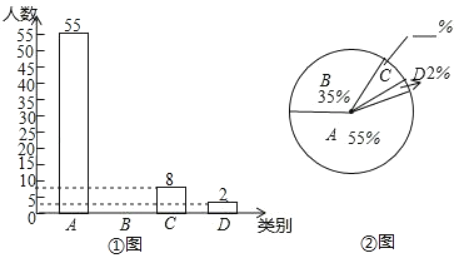
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，二次函数的图象与x轴交于A、B两点，其中A点坐标为，点，另抛物线经过点，M为它的顶点．

    求抛物线的解析式；

    求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，点A，B的坐标分别为（0，4），（﹣3，0），E为AB的中点，EF∥AO交OB于点F，AF与EO交于点P，则EP的长为_____．

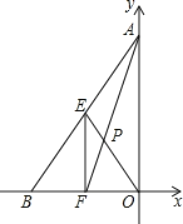
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于反比例函数y＝（k≠0），下列所给的四个结论中，正确的是（　　）

    A. 若点（2，4）在其图象上，则（﹣2，4）也在其图象上

    B. 当k＞0时，y随x的增大而减小

    C. 过图象上任一点P作x轴、y轴的垂线，垂足分别A、B，则矩形OAPB的面积为k

    D. 反比例函数的图象关于直线y＝x和y＝﹣x成轴对称

    查看答案和解析>>

    科目：初中数学 来源： 题型：

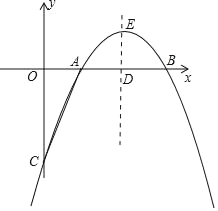
    【题目】如图所示，已知抛物线y＝﹣x2+bx+c与x轴相交于A、B两点，且点A的坐标为（1，0），与y轴交于点C，对称轴直线x＝2与x轴相交于点D，点P是抛物线对称轴上的一个动点，以每秒1个单位长度的速度从抛物线的顶点E向下运动，设点P运动的时间为t（s）．

    （1）点B的坐标为　 　，抛物线的解析式是　 　；

    （2）求当t为何值时，△PAC的周长最小？

    （3）当t为何值时，△PAC是以AC为腰的等腰三角形？

    查看答案和解析>>

    同步练习册答案