
分析 (1)根据中途中途下车了一半人可知车上剩余的人数是$\frac{1}{2}$(6a-6b)人,由于又上车了(7a-3b)人,故把两式相加即可;
(2)把a=200,b=10代入7a-3b即可.
解答 解:(1)∵火车上原有(6a-6b)人,中途下车了一半人,又上车了(7a-3b)人,
∴此时车上共有乘客=$\frac{1}{2}$(6a-6b)+(7a-3b)=3a-3b+7a-3b=(10a-6b)人.
答:此时车上共有乘客共有(10a-6b)人;
(2)a=200,b=100时,7a-3b=7×200-3×100=1400-300=1100(人).
答:中途上车的乘客有1100人.
点评 本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
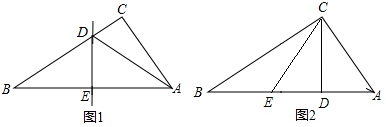
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
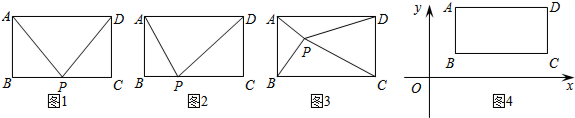
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com