练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，已知AB∥ED，∠B=50°，CN是∠BCE的平分线，CM⊥CN，求∠MCD的度数．

    分析 根据平行线的性质可计算出∠BCE=180°-∠B=130°，再根据角平分线定义得到∠ECN=$\frac{1}{2}$∠BCE=65°，然后利用平角的定义计算∠MCD的度数．

    解答 解：∵AB∥ED，
    ∴∠BCE=180°-∠B=180°-50°=130°，
    ∵CN是∠BCE的平分线，
    ∴∠ECN=$\frac{1}{2}$∠BCE=65°，
    ∵CM⊥CN，
    ∴∠MCN=90°，
    ∴∠MCD=180°-90°-65°=25°．

    点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．计算：（2$\sqrt{6}$-2）10•（5+2$\sqrt{6}$）10=$（6\sqrt{6}+14）^{10}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

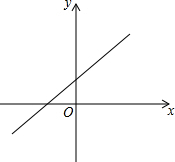    5．已知二次函数y1=x2-2x-3及一次函数y2=x+m，将该二次函数图象在x轴下方的部分沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象，求新图象与直线y2=x+m有三个不同公共点时m的值1或$\frac{13}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，已知直线AB∥CD，试确定∠A，∠F，∠C与∠E，∠G之间的数量关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，B坐标为（2，0），AB⊥x轴于B，△ABO的面积为3．
    （1）求直线AO的解析式；
    （2）将B点向上平移2个单位得到C点，点C是否在y=$\frac{x}{2}$+1的图象上，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

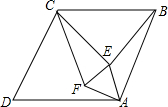    19．如图，在菱形ABCD中，∠D=60°，点E、F在菱形ABCD内部，△AEF为等边三角形．
    （1）求证：BE=CF；
    （2）若AE=6，BE=10，CE=8，求∠AEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

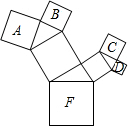    6．若图中正方形F以上的正方形均是以直角三角形向外作的正方形：
    （1）若正方形A，B，C，D的边长分别是a，b，c，d，则正方形F的面积如何用a，b，c，d的式子表示出来为F的面积=a2+b2+c2+d2；
    （2）如果正方形F的边长16cm，那么正方形A，B，C，D的面积之和是256cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．如图，△ADE≌△BCF，∴AE=BF，
    AD=BC，
    DE=CF，
    ∠AED=∠BFC，
    ∠ADE=∠BCF，
    ∠DAE=∠CBF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．若（3x-y+5）2+|2x-y+3|=0，则x+y的值为（　　）
    A．2B．-3C．-1D．3

    查看答案和解析>>

    同步练习册答案