
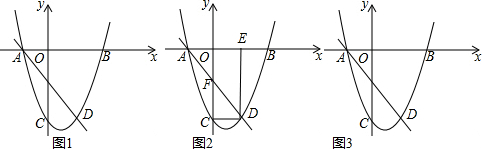
·ЦОц ЈЁ1Ј©ЗуіцөгAЧшұкЈ¬°СAЎўBЎўCИэөгҙъИлЕЧОпПЯҪвОцКҪҪв·ҪіМЧйјҙҝЙЈ®
ЈЁ2Ј©·ЦИэЦЦЗйРОМЦВЫўЩөұQөгФЪCDЙПКұўЪөгQФЪCOЙПКұўЫөгQФЪOEЙПКұЈ¬АыУГПаЛЖИэҪЗРОөДРФЦКВ·іМ·ҪіМЗуіцtЈ¬ІўЗТЕР¶ПКЗ·с·ыәПМвТвјҙҝЙЈ®
ЈЁ3Ј©ИзНј4ЦРУРЛДЦЦЗйРОЈ¬·ЦұрёщҫЭЖҪРРЛДұЯРОөДРФЦК»тАыУГТ»ҙОәҜКэөДРФЦКҪвҫцЈ®
Ҫвҙр ҪвЈәЈЁ1Ј©Боy=0Ј¬Фт-2x-2=0Ј¬ҪвөГx=-1Ј¬ЛщТФөгAЧшұкЈЁ-1Ј¬0Ј©Ј¬
ЙиЕЧОпПЯҪвОцКҪОӘy=ax2+bx+cЈ¬
ЎЯAЈЁ-1Ј¬0Ј©ЎўBЈЁ3Ј¬0Ј©ЎўCЈЁ0Ј¬-6Ј©ФЪЕЧОпПЯЙПЈ¬
Ўа$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c+0}\\{c=-6}\end{array}\right.$Ј¬ҪвөГ$\left\{\begin{array}{l}{a=2}\\{b=-4}\\{c=-6}\end{array}\right.$Ј¬
ЎаЕЧОпПЯҪвОцКҪОӘy=2x2-4x-6Ј®
ЈЁ2Ј©y=2x-2Ј¬Боx=0Ј¬y=-2Ј¬ЎаFЈЁ0Ј¬-2Ј©Ј¬
УЙ$\left\{\begin{array}{l}{y=-2x-2}\\{y=2{x}^{2}-4x-6}\end{array}\right.$ҪвөГ$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.\\;»т\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$»т$\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$Ј¬
ЎаөгDЧшұкЈЁ2Ј¬-6Ј©Ј®ЎЯөгCЈЁ0Ј¬-6Ј©Ј¬
ЎаCDЎНCFЈ¬
ЎаЎПDCF=90ЎгЈ¬
УЙМвТвЈәPөгТЖ¶ҜөДВ·іМОӘDP=tЈ¬QөгТЖ¶ҜөДВ·іМОӘ3ЈЁt-1Ј©=3t-3Ј¬
өұQөгФЪCDЙПКұЈ¬јҙ0Јј3t-3ЎЬ2КұЈ¬1ЈјtЎЬ$\frac{5}{3}$КұЈ¬
ИзНј1ЦРЈ¬ИфPQЎНDFЈ¬ФтУРRTЎчQDPЎЧRTЎчFCDЈ¬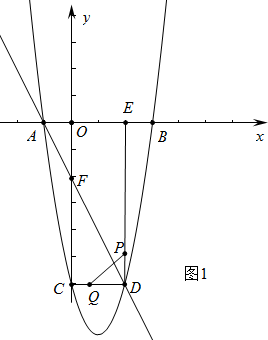
Ўа$\frac{PD}{QD}$=$\frac{CD}{CF}$Ј¬јҙ$\frac{t}{3t-3}$=$\frac{1}{2}$Ј¬
Ўаt=3Ј¬3Јҫ$\frac{5}{3}$Ј¬
ЎаҙЛКұtІ»әПМвТвЈ®
өұөгQФЪCOЙПКұЈ¬2Јј3t-3ЎЬ8Ј¬$\frac{5}{3}$ЈјtЎЬ$\frac{11}{3}$КұЈ¬ИзНј2ЦРЈ¬№эөгPЧчPKЎНOCУЪKЈ¬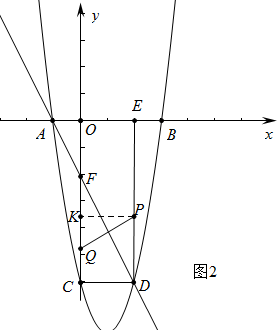
ЎаCK=PD=tЈ¬CQ=3ЈЁt-1Ј©-2=3t-5Ј¬
ИфPQЎНDFЈ¬ФтУРRTЎчPKQЎЧRTЎчFCDЈ¬
Ўа$\frac{QK}{PK}=\frac{CD}{CF}$Ј¬јҙ$\frac{-2t+5}{2}$=$\frac{2}{4}$Ј¬
Ўаt=2Ј¬ЎЯ$\frac{5}{3}$ЈјtЎЬ$\frac{11}{3}$Ј¬
Ўаt=2·ыәПМвТвЈ®
өұөгQФЪOEЙПКұЈ¬јҙ8ЎЬ3t-3ЎЬ10Ј¬$\frac{11}{3}$ЎЬtЎЬ$\frac{13}{3}$КұЈ¬ИзНј3ЦРЈ¬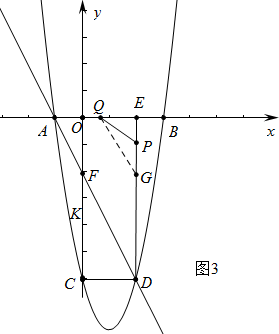
ИфPQЎНDFЈ¬№эөгQЧчQGЎОDFҪ»DEУЪGЈ¬ФтQGЎНQPЈ¬јҙЎПGQP=90ЎгЈ¬
ЎаЎПQPEЈҫ90ЎгЈ¬ХвУлЎчQPEДЪҪЗәНОӘ180ЎгГ¬¶ЬЈ¬ҙЛКұPQІ»УлDFҙ№ЦұЈ¬
ЧЫЙПЛщКцЈәөұt=2КұЈ¬УРPQЎНDFЈ®
ЈЁ3Ј©ИзНј4ЦРЈ¬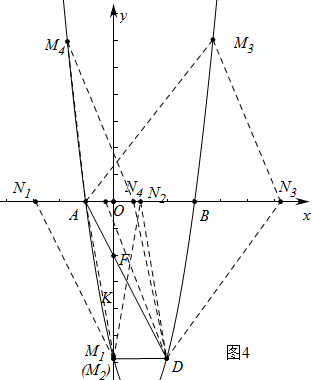
ўЩөұM1N1ЎОADЈ¬AN1ЎОDM1КұЈ¬AN1=DM1=2Ј¬ҙЛКұN1ЧшұкЈЁ-3Ј¬0Ј©Ј¬
ўЪөұADОӘ¶ФҪЗПЯКұЈ¬ЎЯAN2=DM2=2Ј¬
ЎаөгN2ЧшұкОӘЈЁ1Ј¬0Ј©Ј¬
ўЫөұADЎОN3M3Ј¬AD=M3N3КұЈ¬ҙЛКұөгM3өДЧЭЧшұкОӘ6Ј¬өұADЎОM4N4Ј¬AD=M4N4КұЈ¬ҙЛКұөгM4өДЧЭЧшұкОӘ6Ј¬
Ј¬Боy=6Ј¬Фт2x2-4x-6=6Ј¬ҪвөГx=1$ЎА\sqrt{7}$Ј¬
ЎаM3ЈЁ1+$\sqrt{7}$Ј¬6Ј©Ј¬M4ЈЁ1-$\sqrt{7}$Ј¬0Ј©Ј¬
ЦұПЯM3N3ОӘЈәy=-2x+8+2$\sqrt{7}$Ј¬ЦұПЯM4N4ОӘЈәy=-2x+8-2$\sqrt{7}$Ј¬
ЎаN3ЈЁ4+$\sqrt{7}$Ј¬0Ј©Ј¬N4ЈЁ4-$\sqrt{7}$Ј¬0Ј©Ј¬
ЧЫЙПЛщКцөгNЧшұкОӘЈЁ-3Ј¬0Ј©Ј¬ЈЁ1Ј¬0Ј©Ј¬ЈЁ4+$\sqrt{7}$Ј¬0Ј©Ј¬ЈЁ4-$\sqrt{7}$Ј¬0Ј©Ј®
өгЖА ұҫМвҝјІй¶юҙОәҜКэөДУР№ШЦӘК¶Ј¬С§»бҙэ¶ЁПөКэ·ЁИ·¶ЁәҜКэҪвОцКҪЈ¬ҪвМвөД№ШјьКЗ»б·ЦАаМЦВЫЈ¬јмСйКЗ·с·ыәПМвТвЈ¬өЪИэёцОКМвРиТӘ»ӯіцНјРОЈ¬АыУГЖҪРРЛДұЯРОөДРФЦК»бТ»ҙОәҜКэИ·¶ЁөгNөДЧшұкЈ¬КфУЪЦРҝјС№ЦбМвЈ®


 јвЧУЙъРВҝОМГҝОКұЧчТөПөБРҙр°ё
јвЧУЙъРВҝОМГҝОКұЧчТөПөБРҙр°ё УўІЕјЖ»®Н¬ІҪҝОКұёЯР§СөБ·ПөБРҙр°ё
УўІЕјЖ»®Н¬ІҪҝОКұёЯР§СөБ·ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
| AЈ® | ўЩўЪ | BЈ® | ўЩўЫ | CЈ® | ўЩўЪўЬ | DЈ® | ўЪўЫўЬ |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
 РЎГч°пЦъЧцЙъТвөДёёЗЧХыАнІЦҝвЈ¬ФЪІЦҝвөДТ»ҪЗХыЖлөШ¶С·ЕЧЕИфёЙёцПаН¬өДХэ·ҪМе»хПдЈ¬ИзНјКЗРЎГч»ӯіцөДХв¶С»хПдөДИэЦЦКУНјЈ¬Хв¶СХэ·ҪМе»хПд№ІУРЈЁЎЎЎЎЈ©
РЎГч°пЦъЧцЙъТвөДёёЗЧХыАнІЦҝвЈ¬ФЪІЦҝвөДТ»ҪЗХыЖлөШ¶С·ЕЧЕИфёЙёцПаН¬өДХэ·ҪМе»хПдЈ¬ИзНјКЗРЎГч»ӯіцөДХв¶С»хПдөДИэЦЦКУНјЈ¬Хв¶СХэ·ҪМе»хПд№ІУРЈЁЎЎЎЎЈ©| AЈ® | 11Пд | BЈ® | 10Пд | CЈ® | 9Пд | DЈ® | 8Пд |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
 ИзНјЈ¬КЗДіөШ2ФВ18ИХөҪ23ИХPM2.5ЕЁ¶ИөДНіјЖНјЈ¬ФтХвБщМмЦРPM2.5ЕЁ¶ИөДЦРО»КэКЗ79.5ҰМg/m2Ј®
ИзНјЈ¬КЗДіөШ2ФВ18ИХөҪ23ИХPM2.5ЕЁ¶ИөДНіјЖНјЈ¬ФтХвБщМмЦРPM2.5ЕЁ¶ИөДЦРО»КэКЗ79.5ҰМg/m2Ј®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
 ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ЕЧОпПЯy=x2+bx+cУлxЦбПаҪ»УЪөгAәНөгBЈ¬ТСЦӘөгAөДЧшұкОӘЈЁ1Ј¬0Ј©Ј¬УлyЦбПаҪ»УЪөгCЈЁ0Ј¬3Ј©Ј¬ЕЧОпПЯөД¶ҘөгОӘPЈ®
ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ЕЧОпПЯy=x2+bx+cУлxЦбПаҪ»УЪөгAәНөгBЈ¬ТСЦӘөгAөДЧшұкОӘЈЁ1Ј¬0Ј©Ј¬УлyЦбПаҪ»УЪөгCЈЁ0Ј¬3Ј©Ј¬ЕЧОпПЯөД¶ҘөгОӘPЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
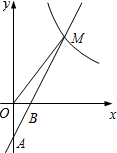 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬Т»ҙОәҜКэy=kx+bЈЁkЎЩ0Ј©өДНјПуҫӯ№эAЈЁ0Ј¬-2Ј©Ј¬BЈЁ1Ј¬0Ј©БҪөгЈ¬Ул·ҙұИАэәҜКэy=$\frac{m}{x}$ЈЁmЎЩ0Ј©өДНјПуФЪөЪТ»ПуПЮДЪҪ»УЪөгMЈ¬ИфЎчOBMөДГж»эКЗ2Ј®
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬Т»ҙОәҜКэy=kx+bЈЁkЎЩ0Ј©өДНјПуҫӯ№эAЈЁ0Ј¬-2Ј©Ј¬BЈЁ1Ј¬0Ј©БҪөгЈ¬Ул·ҙұИАэәҜКэy=$\frac{m}{x}$ЈЁmЎЩ0Ј©өДНјПуФЪөЪТ»ПуПЮДЪҪ»УЪөгMЈ¬ИфЎчOBMөДГж»эКЗ2Ј®Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com