
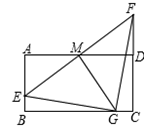
如图在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上的一动点,连接EM并延长交CD的延长线于点F,G是线段BC上的一点,连接GE 、GF、GM .若△EGF是等腰直角三角形, =90°,则AB=
=90°,则AB=
科目:初中数学 来源: 题型:
如图,E是边长为l的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值为( )

A. B.
B.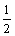 C.
C. D.
D.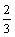
查看答案和解析>>
科目:初中数学 来源: 题型:
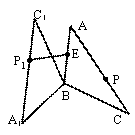
如图,在⊿ABC中,∠A﹤90°,∠C=30°,AB=4,BC=6,E为AB的中点,P为AC边上一动点,将⊿ABC绕点B逆时针旋转 角(
角(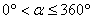 )得到
)得到 ,点P的对应点为
,点P的对应点为
 ,连
,连 ,在旋转过程中,线段
,在旋转过程中,线段 的长度的最小值是 .
的长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,设∠BAC=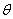 (0°<
(0°<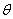 <90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A
<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点A 开始,用等长的小棒依次向右摆放,其中 A
开始,用等长的小棒依次向右摆放,其中 A A
A 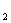 为第一根小棒,且 A
为第一根小棒,且 A A
A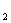 =AA
=AA

(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则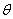 1 = ,
1 = ,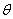 2= ,
2= , 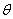 3= ;(用含
3= ;(用含 的式子表示)
的式子表示)
(3)若只能摆放4根小棒,求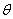 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
在矩形ABCD中,AB=1,AD=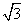 ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE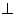 BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
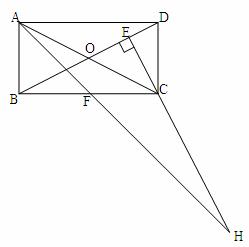
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:初中数学 来源: 题型:
某学校为了绿化校 园,决定从某苗圃购进甲、乙、丙三种树苗共80株,其中甲种树苗株树是乙种树苗株树的2倍,购买三种树苗的总金额不超过1320元,已知乙种树苗的单价是16元/
园,决定从某苗圃购进甲、乙、丙三种树苗共80株,其中甲种树苗株树是乙种树苗株树的2倍,购买三种树苗的总金额不超过1320元,已知乙种树苗的单价是16元/ 株,乙种树苗的单价是甲种树苗的单价的
株,乙种树苗的单价是甲种树苗的单价的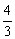 ,购买丙种树苗12株的金额等于购买甲种树
,购买丙种树苗12株的金额等于购买甲种树 苗20株的金额。
苗20株的金额。
(1) 甲、丙两种树苗的单价分别是多少元?
甲、丙两种树苗的单价分别是多少元?
(2)若要求甲种 树苗的株树不超过丙种树苗的株树,请你帮助设计共有哪些购买方案?
树苗的株树不超过丙种树苗的株树,请你帮助设计共有哪些购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com