
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() ,点
,点![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 上的动点,当
上的动点,当![]() 的周长最小时,
的周长最小时,![]() 的度数是______________.
的度数是______________.
【答案】![]()
【解析】
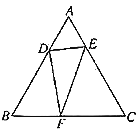
先作点D关于AC和BC的对称点G、H,连接GH交AC和BC于点E、F,此时△DEF的周长最小,再根据三角形内角和与等腰三角形的性质即可求解.
解:如图,作点D关于AC的对称点G,点D关于BC的对称点H,连接GH交AC、BC于E、F,

∵D、G关于AC对称,D、H关于BC对称,
∴DE=EG,DF=FH,
∴![]() 的周长=DE+DF+EF=EG+EF+FH,
的周长=DE+DF+EF=EG+EF+FH,
∴当G、E、F、H四个点在同一直线上时,![]() 的周长最小,
的周长最小,
∵![]() 是等边三角形,
是等边三角形,
∴∠A=∠B = ![]() ,
,
∵D、G关于AC对称,D、H关于BC对称,
∴∠ADG= ![]() ,∠BDH=
,∠BDH= ![]() ,∠EDG=∠DGE,∠FDH=∠DHF,
,∠EDG=∠DGE,∠FDH=∠DHF,
∴∠GDH=![]() ,
,
∴∠DGE+∠DHF=![]() ,
,
∴∠EDG+∠FDH=![]() ,
,
∴∠EDF=![]() .
.
故答案是:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(综合与实践
如图,直线![]() 的函数关系式为
的函数关系式为![]() ,且
,且![]() 与
与![]() 轴交于点A,直线
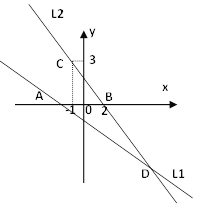
轴交于点A,直线![]() 经过点B(2,0),C(-1,3),直线
经过点B(2,0),C(-1,3),直线![]() 与
与![]() 交于点D.
交于点D.
(1)求直线![]() 的函数关系式;
的函数关系式;
(2)求△ABD的面积.
(3)点P是![]() 轴上一动点,问是否存在一点P,恰好使△ADP为直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上一动点,问是否存在一点P,恰好使△ADP为直角三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生每天参加户外活动的情况,随机抽查了100名学生每天参加户外活动的时间情况,并将抽查结果绘制成如图所示的扇形统计图.
请你根据图中提供的信息解答下列问题:

(1)请直接写出图中![]() 的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
的值,并求出本次抽查中学生每天参加户外活动时间的中位数;
(2)求本次抽查中学生每天参加户外活动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘被等分成六个扇形区域,并在上面依次写上数字:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .转盘指针的位置固定,转动转盘后任其自由停止.
.转盘指针的位置固定,转动转盘后任其自由停止.
![]() 当停止转动时,指针指向奇数区域的概率是多少?
当停止转动时,指针指向奇数区域的概率是多少?
![]() 请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为
请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为![]() ,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)
,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com