
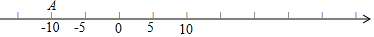 ��1��������ijһ��������Ӧ����Ϊ2����һ�����Ӧ����Ϊ-8����������֮��ľ���Ϊ10��
��1��������ijһ��������Ӧ����Ϊ2����һ�����Ӧ����Ϊ-8����������֮��ľ���Ϊ10������ ��1�����������ľ��빫ʽ�������������֮��ľ��룻
��2�����ݵ�A��B��C֮��Ĺ�ϵ�����ҳ���C��B��Ӧ������
���ҳ��˶�ʱ��Ϊt��ʱ����P��Q��ʾ�������ٸ��������ľ��빫ʽ���ɵó�����t������ֵ���ŵ�һԪһ�η��̣���֮���ɵó����ۣ�
�ڸ��ݢٵĽ��۽��·��=�ٶȡ�ʱ�伴�ɵó�����m��һԪһ�η��̣���֮���ɵó����ۣ�
��� �⣺��1��������֮��ľ���Ϊ2-��-8��=10��
�ʴ�Ϊ10��
��2���������ϵ���-10��Ӧ�ĵ�ΪA����Bλ��A����ұߣ���A��m�����ȵ�λ��CΪ�߶�AB�ϵ�һ�㣬AC=2BC��
���B��Ӧ����Ϊm-10����C��Ӧ����Ϊ$\frac{2}{3}$m-10��
�ٵ��˶�ʱ��Ϊt��ʱ����P��Ӧ����Ϊ3t-10����Q��Ӧ�ĵ�Ϊm-2t-10��
��P��Q��C�������ͬ��
��|$\frac{2}{3}$m-10-��3t-10��|=|$\frac{2}{3}$m-10-��m-2t-10��|��
��ã�t1=$\frac{m}{3}$��t2=$\frac{m}{5}$����
�൱P��Q��C�������ͬʱ���˶�ʱ��tΪ$\frac{m}{3}$���$\frac{m}{5}$�룮
���ɢٿ�֪����t=$\frac{m}{5}$��ʱ����P��Q�غϣ�
�ߵ�������Qͨ��C��1������������P������
��2•��$\frac{m}{5}$-1��=$\frac{1}{3}$m��
��ã�m=30��
������������Qͨ��C��1������������P������m��ֵΪ30��
���� ���⿼����һԪһ�η��̵�Ӧ�á������Լ�����֮��ľ��룬����Ĺؼ��ǣ���1�����������ľ��빫ʽ��������ľ��룻��2���ٸ��������ľ��빫ʽ�г�����t������ֵ���ŵ�һԪһ�η��̣��ڸ���������ϵ·��=�ٶȡ�ʱ���г�����m��һԪһ�η��̣�


 53���ò�ϵ�д�
53���ò�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 8 | C�� | ��4 | D�� | ��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20 | B�� | -16 | C�� | 20��-16 | D�� | -20��16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���ֱ��y=3x��y������ƽ�ƺ�õ�ֱ��AB�������N��m��n����ֱ��AB�ϵ�һ�㣬��3m-n=2����ôֱ��AB�ĺ�������ʽΪy=3x-2��
��ͼ����ƽ��ֱ������ϵ�У���ֱ��y=3x��y������ƽ�ƺ�õ�ֱ��AB�������N��m��n����ֱ��AB�ϵ�һ�㣬��3m-n=2����ôֱ��AB�ĺ�������ʽΪy=3x-2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com