
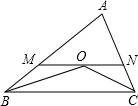
 已知:如图,△AMN的周长为18,∠B,∠C的平分线相交于点O,过O点的直线MN∥BC交AB、AC于点M、N.求AB+AC的值.
已知:如图,△AMN的周长为18,∠B,∠C的平分线相交于点O,过O点的直线MN∥BC交AB、AC于点M、N.求AB+AC的值. 分析 由∠B,∠C的平分线相交于点O,过O点的直线MN∥BC交AB、AC于点M、N,易证得△BOM与△CON是等腰三角形,继而可得AB+AC=△AMN的周长.
解答 解:∵MN∥BC,
∴∠BOM=∠OBC,∠CON=∠OCB,
∵∠B,∠C的平分线相交于点O,
∴∠MBO=∠OBC,∠NCO=∠OCB,
∴∠MBO=∠BOM,∠NCO=∠CON,
∴BM=OM,CN=ON,
∵△AMN的周长为18,
∴AM+MN+AN=AM+OM+ON+AN=AM+BM+CN+AN=AB+AC=18.
点评 本题主要考查等腰三角形的判定与性质,平行线的性质以及角平分线的定义.此题难度适中,注意掌握数形结合思想与转化思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
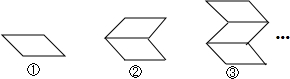
| 图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
| 火柴棒的根数 | 4 | 7 | 10 | 13 | 16 | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com