
【题目】如图,D、E分别是⊙O两条半径OA、OB的中点,![]() .
.
(1)求证:CD=CE.
(2)若∠AOB=120°,OA=x,四边形ODCE的面积为y,求y与x的函数关系式.
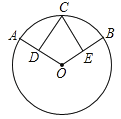
【答案】(1)证明见解析;(2)y=![]() x2.
x2.
【解析】
(1)连接OC,根据圆心角、弧、弦的关系定理得到∠COA=∠COB,证明△COD≌△COE,根据全等三角形的性质证明;
(2)连接AC,根据全等三角形的判定定理得到△AOC为等边三角形,根据正切的定义求出CD,根据三角形的面积公式计算即可.
(1)证明:连接OC,
∵![]() ,
,
∴∠COA=∠COB,
∵D、E分别是⊙O两条半径OA、OB的中点,
∴OD=OE,
在△COD和△COE中,
 ,
,
∴△COD≌△COE(SAS)
∴CD=CE;
(2)连接AC,
∵∠AOB=120°,
∴∠AOC=60°,又OA=OC,
∴△AOC为等边三角形,
∵点D是OA的中点,
∴CD⊥OA,OD=![]() OA=
OA=![]() x,
x,
在Rt△COD中,CD=ODtan∠COD=![]() ,
,
∴四边形ODCE的面积为y=![]() ×OD×CD×2=
×OD×CD×2=![]() x2.
x2.


科目:初中数学 来源: 题型:
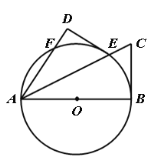
【题目】如图,已知AB是⊙O的直径,F是⊙O上一点,∠BAF的平分线交⊙O于点E,交⊙O的切线BC于点C,过点E作ED⊥AF,交AF的延长线于点D.
(1)求证:DE是⊙O的切线;
(2)若DE=3,CE=2,
①求![]() 值;
值;
②若点G 为AE上一点,求OG+![]() EG最小值.
EG最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
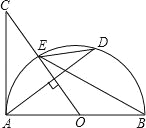
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交半圆O于点E,交AC于点C,使∠BED=∠C.
(1)判断直线AC与圆O的位置关系,并证明你的结论;
(2)若AC=8,cos∠BED=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)如图1,A,B为直线l同侧的两点,过点A作直线l的对称点![]() ,连接
,连接![]() B交直线l于点P,连接AP,则称点P为点A,B关于直线
B交直线l于点P,连接AP,则称点P为点A,B关于直线![]() 的“等角点”.
的“等角点”.
(运用)如图2,在平面直坐标系xOy中,已知A(2,![]() ),B(-2,-
),B(-2,-![]() )两点.
)两点.
(1)C(4,![]() ),D(4,
),D(4,![]() ),E(4,
),E(4,![]() )三点中,点 是点A,B关于直线x=4的等角点;
)三点中,点 是点A,B关于直线x=4的等角点;
(2)若直线l垂直于x轴,点P(m,n)是点A,B关于直线l的等角点,其中m>2,∠APB=α,求证:![]() ;
;
(3)若点P是点A,B关于直线y=ax+b(a≠0)的等角点,且点P位于直线AB的右下方,当∠APB=60°时,求b的取值范围(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被大山阻隔,由A地到B地需要绕行C地,若打通穿山隧道,建成A,B两地的直达高铁,可以缩短从A地到B地的路程.已知:∠CAB=30°,∠CBA=45°,AC=580公里,求隧道打通后与打通前相比,从A地到B地的路程将约缩短多少公里?(参考数据:![]() 1.7,
1.7,![]() 1.4)
1.4)
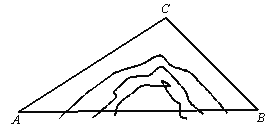
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.
(1)求AC的长;
(2)先将△ABC向右平移2个单位得到△A′B′C′,写出A点的对应点A′的坐标;
(3)再将△ABC绕点C按逆时针方向旋转90°后得到△A1B1C1,写出A点对应点A1的坐标.
(4)求点A到A′所画过痕迹的长.
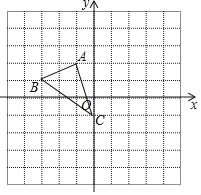
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…都在y轴上,对应的纵坐标分别为1,2,3,….直线l1,l2,l3,…分别经过点A1,A2,A3,…,且都平行于x轴.以点O为圆心,半径为2的圆与直线l1在第一象限交于点B1,以点O为圆心,半径为3的圆与直线l2在第一象限交于点B2,…,依此规律得到一系列点Bn(n为正整数),则点B1的坐标为_____,点Bn的坐标为_____.
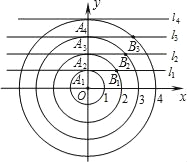
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以点B为圆心,任意长为半径画弧,分别交AB、BC于点M、N分别以点M、N为圆心,以大于![]() MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=
MN的长度为半径画弧两弧相交于点P过点P作线段BD,交AC于点D,过点D作DE⊥AB于点E,则下列结论①CD=ED;②∠ABD=![]() ∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
∠ABC;③BC=BE;④AE=BE中,一定正确的是( )
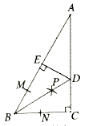
A. ①②③B. ① ② ④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2
(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.求y=-2x2+5x-3函数的“旋转函数”.
小明是这样思考的:由y=-2x2+5x-3函数可知,a1=-2,b1=5,c1=-3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面的问题:
(1)写出函数y=-2x2+5x-3的“旋转函数”;
(2)若函数y1=x2+![]() x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
x-n与y2=-x2-mx-2互为“旋转函数”,求(m+n)2019的值;
(3)已知函数y=![]() (x-2)(x+3)的图像与
(x-2)(x+3)的图像与![]() 轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=
轴交于A、B两点,与y轴交于点C,点A、B、C关于原点的对称点分别是A1、B1、C1,试证明经过点A1、B1、C1的二次函数与函数y=![]() (x-2)(x+3)互为“旋转函数”.
(x-2)(x+3)互为“旋转函数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com