练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．已知一次函数y=kx+b的函数值y随x的增大而增大，且其图象与y轴的负半轴相交，则对k和b的符号判断正确的是（　　）
    A．k＞0，b＞0B．k＞0，b＜0C．k＜0，b＞0D．k＜0，b＜0

    分析 一次函数y=kx+b中y随x的增大而增大，且与y轴负半轴相交，即可确定k，b的符号．

    解答 解：∵一次函数y=kx+b中y随x的增大而增大，
    ∴k＞0，
    ∵一次函数y=kx+b与y轴负半轴相交，
    ∴b＜0．
    故选：B．

    点评 此题主要考查了一次函数图象与系数的关系，一次函数y=kx+b的图象有四种情况：
    ①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限，y的值随x的值增大而增大；
    ②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限，y的值随x的值增大而增大；
    ③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限，y的值随x的值增大而减小；
    ④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限，y的值随x的值增大而减小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．下列各数中3.$\stackrel{••}{14}$，$\frac{1}{2}$π，1.090 090 009…，$\frac{22}{7}$，0，3.1415是无理数的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．在进行二次根式的化简与运算时，如遇到$\frac{3}{\sqrt{5}}$，$\sqrt{\frac{2}{3}}$，$\frac{2}{\sqrt{3}+1}$这样的式子，还需做进一步的化简：
    $\frac{3}{\sqrt{5}}$=$\frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$．①
    $\sqrt{\frac{2}{3}}$=$\sqrt{\frac{2×3}{3×3}}$=$\frac{\sqrt{6}}{3}$．②
    $\frac{2}{\sqrt{3}+1}$=$\frac{2×（\sqrt{3}-1）}{（\sqrt{3}+1）（\sqrt{3}-1）}$=$\frac{2（\sqrt{3}-1）}{（\sqrt{3}）^{2}-{1}^{2}}$=$\sqrt{3}$-1．③
    以上化简的步骤叫做分母有理化．
    $\frac{2}{\sqrt{3}+1}$还可以用以下方法化简：
    $\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{（\sqrt{3}）^{2}-1}{\sqrt{3}+1}$=$\frac{（\sqrt{3}+1）（\sqrt{3}-1）}{\sqrt{3}+1}$=$\sqrt{3}$-1．④
    （Ⅰ）请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$
    （1）参照③式化简$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$
    （2）参照④式化简$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$
    （Ⅱ）化简：$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{2n+1}+\sqrt{2n-1}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，四边形ABCD的对角线互相平分，要使它变为菱形，需要添加的条件是（　　）
    A．AB=CDB．AD=BCC．AC=BDD．AD=CD

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．解方程：$\frac{x+2}{x-1}$-$\frac{4-x}{{x}^{2}-1}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．$|{-\sqrt{2}}|$=（　　）
    A．2B．-2C．$\sqrt{2}$D．-$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．为对荒山进行改造，政府投资13万元给某村民小组用于购买与种植A、B两种树苗共3000棵．完成这项种植后，剩余的款项作为村民小组的纯收入．已知用160元购买A树苗比购买B树苗多3棵．这两种树苗的单价、成活率及移栽费用见下表：
    树苗品种A树苗B树苗
    购买价格（元/棵）aa+12
    树苗成活率90%95%
    移栽费用（元/棵）35
    （1）求表中a的值；
    （2）设购买A树苗x棵，其它购买的是B树苗，把这些树苗种植完成后，村民小组获得的纯收入为y元，请你写出y与x之间的函数关系式；
    （3）若要求这批树苗种植后，成活率达到94%以上（包含94%），则最多种植A树苗多少棵？此时，村民小组在这项工作中，所得的纯收入最大值可以是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）31$\frac{2}{7}$-22$\frac{6}{13}$+4$\frac{5}{7}$+11$\frac{6}{13}$
    （2）（-5.5）+（-3.2）-（-2.5）-4.8
    （3）（-8）×（-25）×（-0.02）
    （4）$\frac{1}{2}$+（-3）2×（-$\frac{1}{2}$）
    （5）8-23÷（-4）3-$\frac{1}{8}$
    （6）100÷（-2）2-（-2）÷（-$\frac{2}{3}$）
    （7）（-3$\frac{1}{7}$）÷（4$\frac{1}{6}$-12$\frac{1}{2}$）÷（-$\frac{11}{25}$）×（-1$\frac{3}{4}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

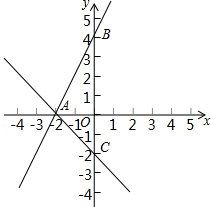    10．如图，已知一次函数y=2x+a与y=-x+b的图象都经过点A（-2，0）且与y轴分别交于B，C两点．
    （1）分别求出这两个一次函数的解析式；
    （2）求△ABC的面积．

    查看答案和解析>>

    同步练习册答案