
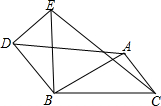
 如图所示,△DBE是△ABC绕点B逆时针旋转后得到的,已知△ABC中,AB=2cm,BC=2.5cm,点A与点D的连线长为2$\sqrt{2}$cm
如图所示,△DBE是△ABC绕点B逆时针旋转后得到的,已知△ABC中,AB=2cm,BC=2.5cm,点A与点D的连线长为2$\sqrt{2}$cm分析 (1)由旋转的性质可知:BD=AB,BE=BC,由勾股定理的逆定理可求得∠DBA=90°;
(2)在△EBC中,由勾股定理可求得EC的长度.
解答 解:(1)由旋转的性质可知:BD=AB=2,BE=BC=2.5.
在△DBA中,$A{D}^{2}=(2\sqrt{2})^{2}=8$,BD2+AB2=22+22=8,
∴AD2=BD2+AB2,
∴∠DBA=90°,即旋转角为90°.
(2)∵∠EBC=∠DBA=90°,
∴△EBC为直角三角形.
∴$EC=\sqrt{B{E}^{2}+B{C}^{2}}$=$\frac{5\sqrt{2}}{2}$.
点评 本题主要考查的是旋转的性质、勾股定理、勾股定理的逆定理的应用,证得∠DBA=90°是解题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
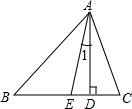 如图,△ABC中,AD是高,AE是角平分线,
如图,△ABC中,AD是高,AE是角平分线,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com