
【题目】某店销售一种小工艺品.该工艺品每件进价12元,售价为20元;每周可售出40件.经调查发现,若把每件工艺品的售价提高1元,就会少售出2件.设每件工艺品售价提高![]() 元,每周从销售这种工艺品中获得的利润为
元,每周从销售这种工艺品中获得的利润为![]() 元.
元.
(1)填空:每件工艺品售价提高![]() 元后的利润为 元,每周售出工品 件,
元后的利润为 元,每周售出工品 件,![]() 关于
关于![]() 的函数关系式为 ;
的函数关系式为 ;
(2)若![]() ,则每件工艺品的售价应确定为多少元?
,则每件工艺品的售价应确定为多少元?
【答案】(1)![]() ;
;![]() ;
;![]() ;(2)售价可定为24元或28元;
;(2)售价可定为24元或28元;
【解析】
(1)根据售价每提高1元其销售量就减少2件可得售价提高x元,则销售量减少2x,根据利润=(售价-进价)×销量列出代数式即可.
(2)根据(1)中所求得出,y=384时,代入y与x关系式,列出方程求解即可.
(1)解:(1)∵该工艺品每件进价12元,售价为20元,
∴每件工艺品售价提高x元后的利润为:(20-12+x)=(8+x)(元),
∵把每件工艺品的售价提高1元,就会少售出2件,
∴每周可售出工艺品:(40-2x)(件),
∴y关于x的函数关系式为:y=(40-2x)(8+x))=-2x2+24x+320;
故答案为:8+x;40-2x;y=-2x2+24x+320;
(2)解:![]()
![]()
![]()
![]()
![]()
![]()
![]() 售价可定为
售价可定为![]() 元或28元
元或28元
答:售价可定为24元或28元


科目:初中数学 来源: 题型:
【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)每件童装降价多少元时,能更多让利于顾客并且商家平均每天能赢利1200元.
(2)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,
,![]() 之间的等量关系.
之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,易证
,易证![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断.
转化在一个三角形中即可判断.
![]() ,
,![]() ,
,![]() 之间的等量关系________;
之间的等量关系________;
(2)问题探究:如图②,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
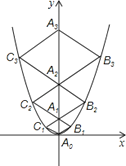
【题目】二次函数y=![]() 的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…Cn在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形,∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An1BnAn
=60°,菱形An﹣1BnAnCn的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
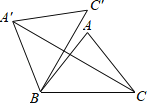
【题目】如图,在△ABC中,AB=AC=5,BC=6,将△ABC绕点B逆时针旋转60°得到△A'BC’,连接A'C,则A'C的长为( )
A. 6B. 4+2![]() C. 4+3
C. 4+3![]() D. 2+3
D. 2+3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
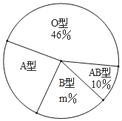
【题目】“只要人人献出一点爱,世界将变成美好的人间”.某大学利用“世界献血日”开展自愿义务献血活动,经过检测,献血者血型有“A、B、AB、O”四种类型,随机抽取部分献血结果进行统计,根据结果制作了如图两幅不完整统计图表(表,图):
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)本次随机抽取献血者人数为 人,图中m= ;
(2)补全表中的数据;
(3)若这次活动中该校有1300人义务献血,估计大约有多少人是A型血?
(4)现有4个自愿献血者,2人为O型,1人为A型,1人为B型,若在4人中随机挑选2人,利用树状图或列表法求两人血型均为O型的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com