
分析 (1)先根据判别式的意义确定n的值,然后根据概率公式求解;
(2)先画树状图展示所有36种等可能的结果数,再找出满足m2-4n>0的结果数,然后根据概率公式求解.
解答 解:(1)当m=4,则△=42-4n>0,解得n<4,所以n可取1、2、3,
所以方程x2+4x+n=0有两个不相等的实数根的概率=$\frac{3}{6}$=$\frac{1}{2}$;
故答案为$\frac{1}{2}$;
(2)画树状图为: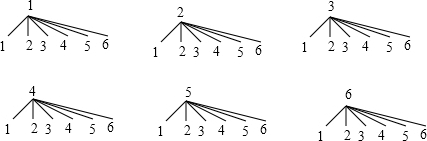
共有36种等可能的结果数,其中满足m2-4n>0的结果数为17,
所以方程x2+mx+n=0有两个不相等的实数根的概率=$\frac{17}{36}$.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.也考查了根的判别式的意义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.
如图,在等边△ABC中,点D在BC边上,点E在AC边上,且∠ADE=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
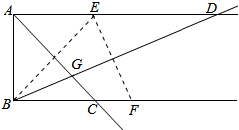 如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )
如图,已知AD∥BC,AB⊥AD,点E、F分别在射线AD、BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则下列结论错误的是( )| A. | tan∠ADB=$\sqrt{2}$-1 | B. | ∠DEF=67.5° | C. | ∠AGB=∠BEF | D. | cos∠AGB=$\frac{\sqrt{6}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com