
分析 (1)根据已知发现前面的数减3得到下一个数,依据此规律可得结果;
(2)根据题意推出规律是从第2个数开始,依次,偶数项-2,奇数项+4;
(3)观察不难发现,分子都是1,分母是从1开始的连续自然数,并且奇数项为负,偶数项为正,然后写出即可.
解答 解:(1)∵1-3=-2,
-2-3=-5,
-5-3=-8,
-8-3=-11,
∴-11-3=-14,
-14-3=-17,
故答案为:-14,-17;
(2)∵-2-2=-4,
-4+4=0,
0-2=-2,
-2+4=2,
∴2-2=0,
0+4=4,
故答案为:0,4;
(3)∵第1项为-1,
第2项为$\frac{1}{2}$,
第3项为$-\frac{1}{3}$,
第4项为$\frac{1}{4}$,
第5项为$-\frac{1}{5}$,
∴第6项为$\frac{1}{6}$,
第7项为$-\frac{1}{7}$,
第2009项为$-\frac{1}{2009}$,
故答案为:$\frac{1}{6}$,$-\frac{1}{7}$,$-\frac{1}{2009}$.
点评 本题主要考查了数字的变化规律,发现规律,运用规律是解答此题的关键.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
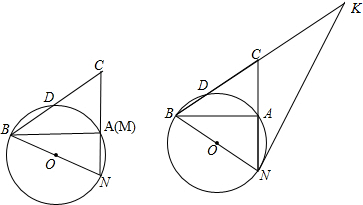
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
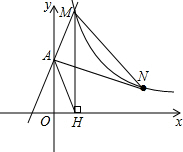 直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MN⊥x轴于点H,OA=2HO.
直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MN⊥x轴于点H,OA=2HO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
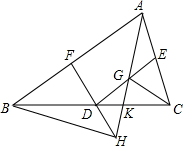 如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH.
如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤2 | B. | x≥2 | C. | x≥-1 | D. | -1≤x≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
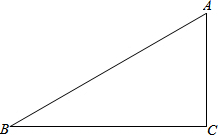 如图,在△ABC中,AB=17,BC=15,AC=8.
如图,在△ABC中,AB=17,BC=15,AC=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com